Pack man
Problem
Atoms can be thought of as hard spheres of a fixed radius, for many purposes in physics.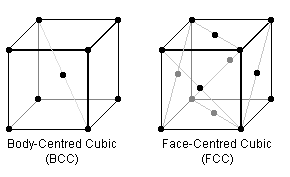
In the BCC & FCC crystal lattice arrangements (the repeating cube of each is pictured above), certain planes are "close packed" i.e. the "hard spheres" are thought of as touching. Steels can have either packing structure, but are generally structurally better in the more densely-packed form which, for example, don't become brittle at low temperatures.
To begin, visualise the crystal arrangements above where the black dots represent the centre of identical spherical atoms of fixed radii which just touch each other.
Can you tell which of BCC or FCC is this better, more dense form? Can you prove it?
Pure copper is structured in the FCC form, has atomic mass 63.5, and atomic radius 128 picometres. Estimate the density of copper. How does your result compare with the actual density of copper?
Student Solutions
The most densely-packed planes for FCC are along the diagonals of the faces of the cube. Thus if the side length is $a$, $\sqrt{2}a = 4\mbox{ radii} \therefore a = \frac{4}{\sqrt{2}}r$. So the fill is $4\mbox{ atoms}/a^3 = \frac{\sqrt{2}\pi}{6} = 74\%\;.$
For BCC, the most densely-packed plane is the inside diagonal, $\therefore \sqrt{3}a = 4\mbox{ radii} \therefore a = \frac{4}{\sqrt{2}} r$. So the fill is $2\mbox{ atoms}/a^3 = \frac{\sqrt{3}\pi}{8} = 68\%\;.$
If you find the FCC side length in terms of the atomic radius of copper, you will find that the answer is very close to the experimentally-found density of copper, $8920\textrm{ kg/m}^3.$
