Kite in a Square
Problem
Kite in a Square printable sheet
ABCD is a square. M is the midpoint of the side AB.
By constructing the lines AC, MC, BD and MD, the blue shaded quadrilateral is formed:
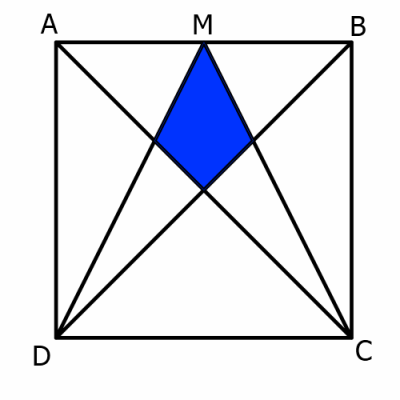
What fraction of the total area is shaded?
Once you have had a think about this, you might like to take a look at these three different methods for finding the shaded area. In each case, all the statements have been muddled up. Can you rearrange them back into their original order?
Thanks to Jerome Foley for drawing our attention to this problem.
Getting Started
For Coordinates approach:
- what are the equations of the lines?
- where do they intersect?
For Similar Figures approach:
- which angles are the same?
- what lengths do we know?
For Pythagoras approach:
- where are the right angles?
- what lengths do we know?
Student Solutions
Viola from St George's British International School, Rome in Italy sent in this elegant method:
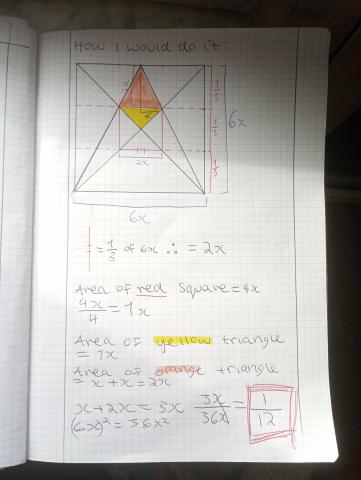
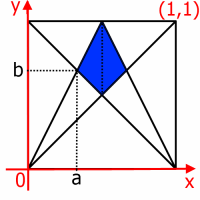
However, Viola has assumed that the vertices of the kite are $\frac12$ and $\frac23$ of the way up the whole square - which might not be true! Zach from Pate's Grammar School in England and Raquel from IES Maximo Laguna in Spain both proved that it is true using coordinates. Below is Raquel's proof that the vertices of the kite are $\frac12$ and $\frac23$ of the way up the whole square:
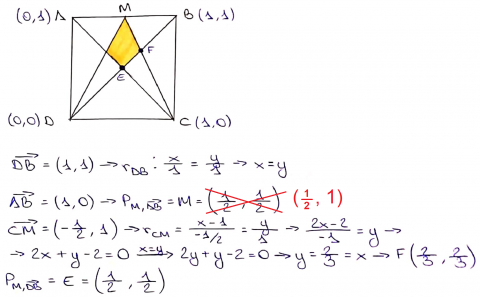
Raquel used this fact to complete a different elegant method:
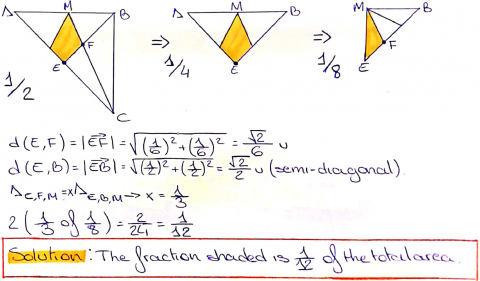
Zach also used coordinates, but Zach worked with a square with sides 10 units long, instead of 1 unit long. Zach also used a different method. Zach began by defining some lengths as $X, Y$ and $Z$:
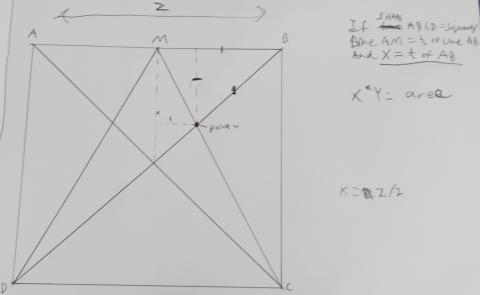
Zach went on to find equations for the lines and line segments. Be careful - sometimes $X$ and $Y$ refer to the coordinates, and sometimes they refer to the lengths defined above.
Rishik K used the three appoaches linked in the problem to compare three different methods. This is Rishik's work:
I enjoyed solving this problem using all the approaches and I believe that they were all smart and interesting methods to work out the shaded area. But I liked the similar figure approach because it was the simplest out of the three and the quote “Mathematics is for lazy people” clearly explains the reason I liked this certain approach.
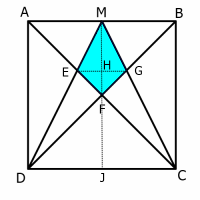
Pythagoras Approach
Coordinates approach
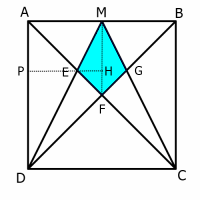
Similar figures approach
Teachers' Resources
Why do this problem?
Students often find geometric proofs quite intractable. In this problem, three different ways of proving the same result are presented, jumbled up, so that students can engage with the proofs without having to start from scratch.
Possible approach
This printable worksheet may be useful: Kite in a Square
These printable cards for sorting may be useful: Coordinates, Similar Triangles, Pythagoras
Show the image from the problem.
"ABCD is a square. M is the midpoint of AB. What fraction of the total area is shaded?"
Give students some time to have a go at the problem. While they are working, circulate and see the methods they are trying.
After a while, bring the class together again and acknowledge that the answer may not be immediately obvious.
"I've been given the methods used by three different people. Unfortunately each method has got jumbled up. Can you put the statements in the right order to build a logical argument?"
Hand out envelopes with each method (Coordinates, Similar Triangles, Pythagoras) to pairs or threes. Coordinates is the most accessible method, and Pythagoras the most
challenging. It is a good idea to print each method on different coloured card to avoid them getting muddled up.
"With your partner, make sense of each step and put the cards in the right order.
Make sure you agree with each other, or that you can convince each other, that the order is right.
Once you've completed the task, can you recreate each method for your partner without looking at the cards?"
Once students have spent enough time engaging with the three methods, making sense of them and recreating them for themselves, bring the class together. Invite pairs students to present each method to the class, and finally discuss the merits and disadvantages of each.
The interactive proof sorters which are available can be used as an alternative to the printable cards, or for students to check their suggested arrangements of the cards.
Key questions
For Coordinates method:
- what are the equations of the lines?
- where do they intersect?
For Similar Figures method:
- which angles are the same?
- what lengths do we know?
For Pythagoras method:
- where are the right angles?
- what lengths do we know?
Possible support
Start by drawing a square on dotty paper (2 by 2 to start with) and explain that vertices and mid-points can be joined with straight lines.
Challenge students to find the different fractions of the square that can be shaded.
Possible extension
Enclosing Squares offers a follow-up activity linked to Coordinates.
Take a Square offers a follow-up activity linked to Similar Figures.
Pythagoras Proofs offers a follow-up activity linked to Pythagoras.