Enclosing Squares
Age 11 to 14
Challenge Level 
Here's a problem to work at with your graphic calculator or graph-plotting package on a computer.
If you plot the following lines
| $\begin{eqnarray} y &=& 2x + 1\\ y &=& 2x + 4 \\ y &=& -0.5x + 1\\ y &=& -0.5x + 2.5 \end{eqnarray}$ |  |
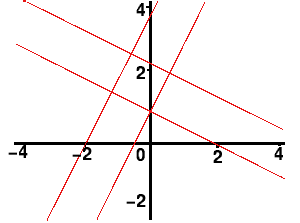
the lines will enclose a square.
Can you find other sets of sloping lines that enclose a square?
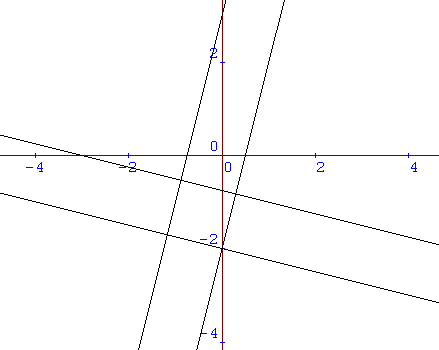
If you are given the equations of two parallel lines
$y = ax + b$ and $y = ax + c$
can you explain how to find the equations of the other two
lines that would enclose a square, if you know that one of the
vertices is at $(0,b)$?
[In the example at the top, $a = 2$, $b = 1$ and $c =
4$]
You may also like
Parallel Lines
How does the position of the line affect the equation of the line? What can you say about the equations of parallel lines?
Reflecting Lines
Investigate what happens to the equations of different lines when you reflect them in one of the axes. Try to predict what will happen. Explain your findings.