Folding Squares
The diagonal of a square intersects the line joining one of the unused corners to the midpoint of the opposite side. What do you notice about the line segments produced?
Problem
Start with a square...
Image

|
Image
|
Image
|
Image
|
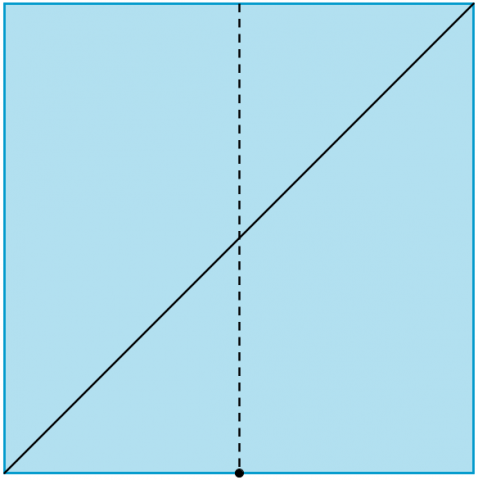
Fold to create a diagonal running from bottom left to top right. |
Find the midpoint of the base by folding. |
Fold the paper again, joining the top left corner to the midpoint of the base. |
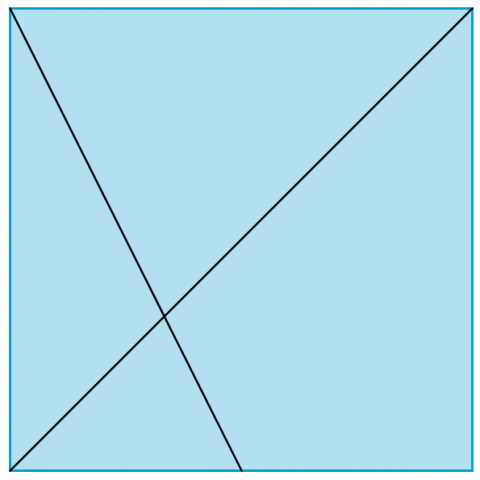
What fractions of the diagonal do you think your new fold has created? |
Measure the two sections of the diagonal and compare their lengths.
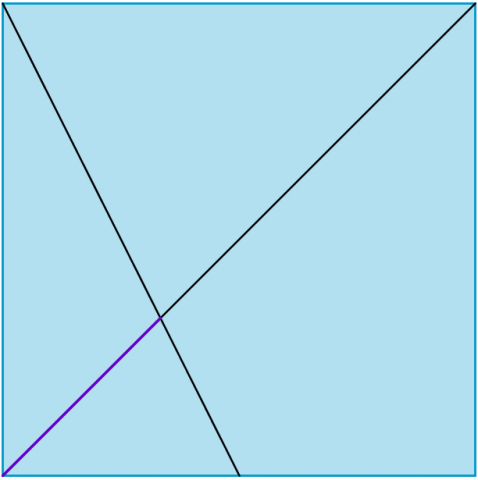
What do you notice?
Is this what you expected?
Is this what you expected?
Can you produce a convincing mathematical argument or proof that justifies what you have found?
You might like to try A Parallelogram Trisection and Folding Fractions next.
Getting Started
Image

Draw some squares and draw in a diagonal plus two lines joining one of the other two vertices to the midpoint of the opposite sides.
What do you notice?
Would this work with a rectangle, a parallelogram, a trapezium?
Student Solutions
Talei from Poltair Community School and Sports College sent in this excellent solution to the problem, showing the diagonals are split in the ratio 1:2 (or equivalently that the smaller part is a third of the whole)
Image

FD = 2EF and FC = 2AF because . . .
We can prove that triangle FCD is an enlargement, by a scale factor of 2, of the triangle AEF.
The triangles' angles are the same - at point F the crossing lines give each triangle an identical angle because they are opposite each other. The line AC joins parallel lines to give an identical angle to each triangle because they are alternate, and the line ED works in the same way.
Therefore, because AE must be exactly half the length of CD, each line in triangle AEF will be half of its enlarged equivalent in triangle FCD.
FD = 2EF because FD is the enlarged equivalent line of EF in triangle AEF.
FC = 2AF because FC is the enlarged equivalent line of AF in triangle AEF.
Talei's method using similar triangles can also be applied to the general case for a pallelogram and arbitary intersection point:
Image

$$\mathrm{\angle afe = \angle cfd \textrm{ (opposite angles) and } \angle eaf = \angle dcf \textrm{ (alternate / 'Z-' angles)}}$$
$$\mathrm{\therefore \triangle aef \textrm{ is similar to }\triangle cdf \Rightarrow \frac{cf}{af} = \frac{cd}{ae} \Rightarrow cf = \frac{cd}{ae}af}$$
$$\mathrm{ac = af + cf \Rightarrow ac = af \left( 1 + \frac{cd}{ae} \right)}$$
$$\mathrm{\therefore \ af = \frac{1}{1 + \frac{cd}{ae}} \textrm{ multiplying through by ae and using cd = ab} \Rightarrow af = \frac{ae}{ae + ab} ac}$$
Teachers' Resources
Why do this problem?
This problem begins with a simple paper fold, which leads to an elegant result. Learners need to estimate lengths and work accurately to construct and measure lines. Once they have made a conjecture it can be justified with geometrical arguments using angles and ratio. To prove the results knowledge of similar
triangles is needed, but the problem could equally well be used as an introduction to the idea of similarity.
Possible approach
Start by giving everyone a square of paper which they can fold according to the diagrams. Encourage them to measure as accurately as possible the two sections of the diagonal which are formed. Collect together some measurements and ask what the learners notice. What do they think would happen with squares of different sizes? In order to collect a lot of data in a short space of time, small
groups could create different sized squares and construct the lines and measure them, sharing the results within their group.
Once a pattern has emerged bring the class together and ask what they have found. Some learners will be convinced that the relationship will always hold because they have tried it with lots of examples, so there is a good opportunity to discuss the distinction between demonstration and mathematical proof.
In order to justify formally what they have noticed, learners might find it useful to discuss what they know to be true, and what a convincing argument shows to be true. This might be for example that certain angles are equal.
Once pairs of equal angles are identified a route to a proof becomes clearer.
The last part of the question asks about other quadrilaterals. Some learners will be secure enough in the proof for squares to attempt to prove or disprove the cases for other quadrilaterals straight away without the need for accurate diagrams or folding.
Key questions
What does it look like the folds are doing to the lines?
How could you verify what you think is true?
What other mathematics do you know that might be useful here?
Does this work for other quadrilaterals?
Possible extension
The problem Folding Fractions builds on these ideas and extends them to different fractions of the line.
