problem
Favourite
Arithmagons
Age
11 to 16
Challenge level
Can you find the values at the vertices when you know the values on the edges?
problem
Favourite
Differences
Age
11 to 14
Challenge level
Can you guarantee that, for any three numbers you choose, the product of their differences will always be an even number?
problem
Favourite
A chance to win?
Age
11 to 14
Challenge level
Imagine you were given the chance to win some money... and imagine
you had nothing to lose...
problem
Favourite
Pair products
Age
14 to 16
Challenge level
Choose four consecutive whole numbers. Multiply the first and last numbers together. Multiply the middle pair together. What do you notice?
problem
Favourite
Warmsnug double glazing
Age
14 to 16
Challenge level
How have "Warmsnug" arrived at the prices shown on their windows? Which window has been given an incorrect price?
problem
Favourite
A little light thinking
Age
14 to 16
Challenge level
Here is a machine with four coloured lights. Can you make two lights switch on at once? Three lights? All four lights?
problem
Favourite
Standard index form matching
Age
14 to 16
Challenge level
Can you match these calculations in Standard Index Form with their answers?
problem
Favourite
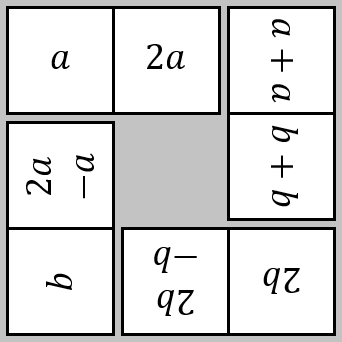
Quad in quad
Age
14 to 18
Challenge level
Join the midpoints of a quadrilateral to get a new quadrilateral. What is special about it?
problem
Favourite
Plus minus
Age
14 to 16
Challenge level
Can you explain the surprising results Jo found when she calculated
the difference between square numbers?
problem
Favourite
Fair shares?
Age
14 to 16
Challenge level
A mother wants to share a sum of money by giving each of her
children in turn a lump sum plus a fraction of the remainder. How
can she do this in order to share the money out equally?
problem
Favourite
What's possible?
Age
14 to 16
Challenge level
Many numbers can be expressed as the difference of two perfect squares. What do you notice about the numbers you CANNOT make?
problem
Favourite
Attractive tablecloths
Age
14 to 16
Challenge level
Charlie likes tablecloths that use as many colours as possible, but insists that his tablecloths have some symmetry. Can you work out how many colours he needs for different tablecloth designs?
problem
Favourite
Tiny nines
Age
14 to 16
Challenge level
What do you notice about these families of recurring decimals?
problem
Favourite
Pick's theorem
Age
14 to 16
Challenge level
Polygons drawn on square dotty paper have dots on their perimeter (p) and often internal (i) ones as well. Find a relationship between p, i and the area of the polygons.
problem
Favourite
Triangle in a triangle
Age
14 to 16
Challenge level
Can you work out the fraction of the original triangle that is covered by the inner triangle?
problem
Favourite
Perpendicular lines
Age
14 to 16
Challenge level
Position the lines so that they are perpendicular to each other. What can you say about the equations of perpendicular lines?
problem
Favourite
Nicely similar
Age
14 to 16
Challenge level
If the hypotenuse (base) length is 100cm and if an extra line splits the base into 36cm and 64cm parts, what were the side lengths for the original right-angled triangle?
problem
Favourite
Filling the gaps
Age
14 to 16
Challenge level
Which numbers can we write as a sum of square numbers?