Filling the gaps

Which numbers can we write as a sum of square numbers?

Age

14 to 16

Challenge level

Secondary

NUMBER

Factors, Multiples & Primes

Being curious Being resourceful Being resilient Being collaborative

Problem

Filling the Gaps printable sheet

Charlie has been thinking about which numbers can be written as a sum of two square numbers. He took a $10\times10$ grid, and shaded the square numbers in blue and the sums of two squares in yellow.

A grid with numbers from 1 to 100 in order, with 10 numbers in each row. Cells with square numbers are blue, numbers which are the sum of two squares have their cells yellow, and the remaining cells are white.

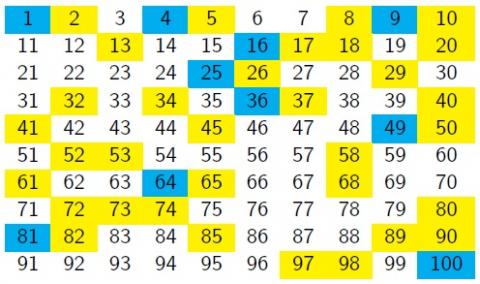
He hoped to find a pattern, but couldn't see anything obvious.

Vicky suggested changing the number of columns in the grid, so they reduced it by one:

A grid with numbers from 1 to 99 in order, with 9 numbers in each row. Cells with square numbers are blue, numbers which are the sum of two squares have their cells yellow, and the remaining cells are white.

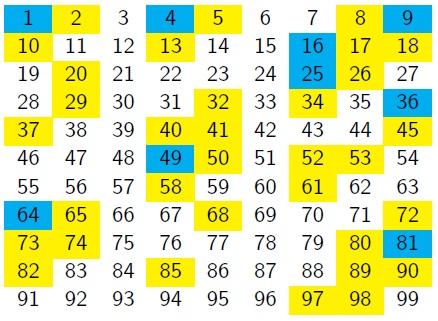
"There seems to be a diagonal pattern."

"If the rows were one shorter, then those diagonals would line up into vertical columns, wouldn't they?"

"Let's try it..."

A grid with numbers from 1 to 96 in order, with 8 numbers in each row. Cells with square numbers are blue, numbers which are the sum of two squares have their cells yellow, and the remaining cells are white.

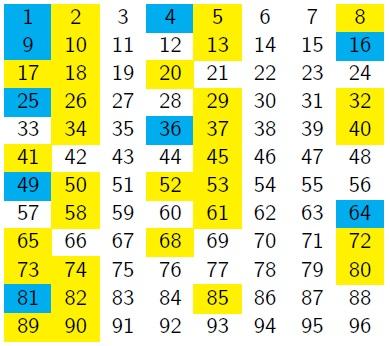
What do you notice about the positions of the square numbers?

What do you notice about the positions of the sums of two square numbers?

Can you make any conjectures about the columns in which squares, and sums of two squares, would appear if the grid continued beyond 96?

Can you prove any of your conjectures?

You might like to look back at the nine-column grid and ask yourself the same questions.

Charlie couldn't write every number as a sum of two squares. He wondered what would happen if he allowed himself three squares.

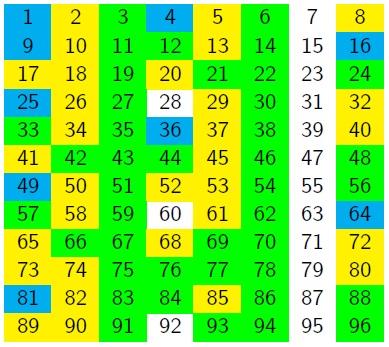
Will any of the numbers in the seventh column be a sum of three squares?

Can you prove it?

"We must be able to write every number if we are allowed to include sums of four squares!"

"Yes, but it's not easy to prove. Several great mathematicians worked on it over a long period before Lagrange gave the first proof in 1770."

With thanks to Vicky Neale who created this task in collaboration with NRICH.

Teachers' Resources

Why do this problem?

This problem provides an interesting context in which students can apply algebraic techniques and ideas about modular arithmetic. It also gives them a taste of an area of number theory that they might study if they go beyond the school curriculum.

Possible approaches

This problem follows on nicely from What Numbers Can We Make?

"Mathematicians have been interested in which numbers can be written as a sum of square numbers. Here are the numbers that we can make as a sum of two squares."

Show grid.

"There don't seem to be any obvious patterns here. But the numbers are only in ten columns because we're used to grids like this. Perhaps we should try a different number of columns instead, like nine."

Show grid.

"Can we see any patterns this time?"

[Students might notice the two empty vertical columns. They might also notice a diagonal pattern (top right to bottom left). Suggest that this diagonal pattern could become vertical if we make each row one shorter.]

Show grid.

Hand out this copy of the grid and give students some time, working in pairs, to look for patterns, make predictions, and explain those predictions. You might want to encourage students to start by looking at the three completely empty columns.

Possible prompts if students are having difficulties providing convincing/rigorous explanations:

In which columns do the square numbers appear?

In which columns do the squares of even numbers appear? Can you explain why?

And the squares of odd numbers? Can you explain why?

How can we describe the numbers in a particular column?

Bring the class together to pool ideas, and then offer this grid with sums of three squares for further investigation. Some students might also like to consider what will happen when we add four squares.

Possible support

Ensure that students have worked on What Numbers Can We Make?

Possible extension

Suggest that students look for patterns that they can explain in the nine-column grid.

Students could also experiment with grids with different numbers of columns.

Filling the gaps

Or search by topic

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Filling the gaps

Problem

Getting Started

Student Solutions

Teachers' Resources

Why do this problem?

Possible approaches

Possible support

Possible extension