Where is the dot?
A dot starts at the point (1,0) and turns anticlockwise. Can you estimate the height of the dot after it has turned through 45 degrees? Can you calculate its height?
Age
14 to 16
Challenge level
Problem
Where is the Dot? printable sheet
Watch the film below.
Imagine the dot starts at the point $(1,0)$ and turns anticlockwise.
Estimate the height of the dot above the horizontal axis after it has turned through $45^\circ$.
Estimate the angle that the dot needs to turn in order to be exactly $0.5$ units above the horizontal axis.
Show how you can use Pythagoras' Theorem to calculate the height of the dot above the horizontal axis after it has turned through $45^\circ$.
Again, without resorting to Trigonometry, calculate the height of the dot above the horizontal axis after it has turned through $30^\circ$ and $60^\circ$?
Are there any other angles for which you can calculate the height of the dot above the horizontal axis?
Getting Started
The radius of the circle is $1$ unit long.
You can use the radius as the hypotenuse of the right-angled triangles.
Student Solutions
The first part of this problem was answered correctly by a
number of people. As the film suggests, we can view the dot as a
vertex on a right angled triangle whose hypotenuse has length one.
The angle $45^{\circ}$ is special because at this point the
triangle is equalateral. Let $x$ denote the height of the dot after
it has turned through $45^{\circ}$.
Image
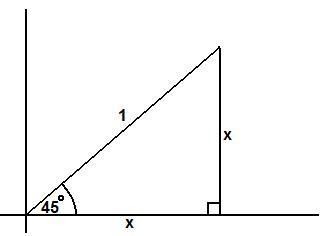
Pythagoras' theorem states that $x^2+x^2=1^2$, i.e. $x^2=\frac{1}{2}$ so $x=\frac{1}{\sqrt{2}}$.
The next part of the question asked for similar ways of calculating the height of the dot after it had turned through $30^{\circ}$ and $60^{\circ}$.
Consider the right angled triangle we obtain after turning through $30^{\circ}$. If we reflect this triangle in the horizontal axis we obtain an equalateral triangle with sides of length $1$ as shown.
Image
This implies that the height of the dot must be $\frac{1}{2}$. We deduce that at $60^{\circ}$ we end up with the following triangle:
Image
By Pythagoras, the height of the dot must satisfy the equation $x^2+(\frac{1}{2})^2=1^2$ which implies that $x=\sqrt{1-\frac{1}{4}}=\sqrt{\frac{3}{4}}=\frac{\sqrt{3}}{2}$.
By symmetry, now that we know the height of the dot for angles of $30^{\circ}$, $45^{\circ}$ and $60^{\circ}$, we can state the height for angles which are a multiple of $30^{\circ}$, $45^{\circ}$ or $60^{\circ}$. See if you can list these angles and the corresponding heights of the dot.
Teachers' Resources
This problem offers students an opportunity to apply Pythagoras' Theorem.
It can also be used as a starting point for trigonometry:
- what happens to the height of the dot during the first $90^{\circ}$ of turn?
- what happens to the height of the dot when it turns beyond $90^{\circ}$?
- what can you say about the horizontal displacement of the dot as it turns through a full circle?