When NRICH started out, the resources were created for, and used mainly by, the highest achieving students.
Twenty five years on, our site has grown and changed, and our target audience is now teachers and students working at all levels. And yet we are still working to shake off the commonly held belief that NRICH is just for top set students...
For many years now, our aim has been, wherever possible, to publish "low threshold high ceiling" tasks that whole classes can work on together. With these tasks, everyone can get started, and everyone can get stuck!
Here are some resources which you might find useful:
Secondary Curriculum
Enriching the Secondary Curriculum
What we think and why we think it
Thinking Mathematically
Posters for the classroom.
Teachers can Register for the NRICH email newsletter to be kept up to date with our latest news.
Below are some of our favourite "low threshold high ceiling" tasks for secondary students.
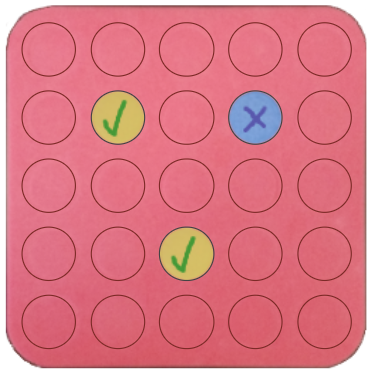
Poly Plug Rectangles
Age 5 to 11
Challenge Level
The computer has made a rectangle and will tell you the number of spots it uses in total. Can you find out where the rectangle is?
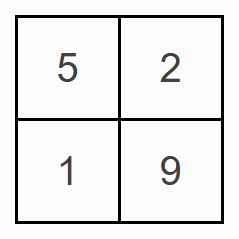
Reach 100
Age 7 to 11
Challenge Level
Choose four different digits from 1-9 and put one in each box so that the resulting four two-digit numbers add to a total of 100.
Shifting Times Tables
Age 11 to 14
Challenge Level
Can you find a way to identify times tables after they have been shifted up or down?
Odds, Evens and More Evens
Age 11 to 14
Challenge Level
Alison, Bernard and Charlie have been exploring sequences of odd and even numbers, which raise some intriguing questions...
Magic Letters
Age 11 to 14
Challenge Level
Charlie has made a Magic V. Can you use his example to make some more? And how about Magic Ls, Ns and Ws?
Polygon Rings
Age 11 to 14
Challenge Level
Join pentagons together edge to edge. Will they form a ring?
Tilted Squares
Age 11 to 14
Challenge Level
It's easy to work out the areas of most squares that we meet, but what if they were tilted?
Summing Consecutive Numbers
Age 11 to 14
Challenge Level
15 = 7 + 8 and 10 = 1 + 2 + 3 + 4. Can you say which numbers can be expressed as the sum of two or more consecutive integers?
Unequal Averages
Age 11 to 14
Challenge Level
Play around with sets of five numbers and see what you can discover about different types of average...
Charlie's Delightful Machine
Age 11 to 16
Challenge Level
Here is a machine with four coloured lights. Can you develop a strategy to work out the rules controlling each light?
Cyclic Quadrilaterals
Age 11 to 16
Challenge Level
Draw some quadrilaterals on a 9-point circle and work out the angles. Is there a theorem?
Factorising with Multilink
Age 14 to 16
Challenge Level
Can you find out what is special about the dimensions of rectangles you can make with squares, sticks and units?
Steel Cables
Age 14 to 16
Challenge Level
Some students have been working out the number of strands needed for different sizes of cable. Can you make sense of their solutions?
Pair Productslive
Age 14 to 16
Challenge Level
Choose four consecutive whole numbers. Multiply the first and last numbers together. Multiply the middle pair together. What do you notice?
Hollow Squares
Age 14 to 16
Challenge Level
Which armies can be arranged in hollow square fighting formations?
Odds and Evens Made Fair
Age 14 to 16
Challenge Level
In this follow-up to the problem Odds and Evens, we invite you to analyse a probability situation in order to find the general solution for a fair game.
NRICH is part of the family of activities in the Millennium Mathematics Project.