Put operations signs between the numbers 3 4 5 6 to make the highest possible number and lowest possible number.
Can you replace the letters with numbers? Is there only one solution in each case?
How can you arrange the 5 cubes so that you need the smallest number of Brush Loads of paint to cover them? Try with other numbers of cubes as well.
What happens when you round these numbers to the nearest whole number?
Use your knowledge of place value to try to win this game. How will you maximise your score?
Cut differently-sized square corners from a square piece of paper to make boxes without lids. Do they all have the same volume?
Can you go through this maze so that the numbers you pass add to exactly 100?
The ancient Egyptians were said to make right-angled triangles using a rope with twelve equal sections divided by knots. What other triangles could you make if you had a rope like this?
Find at least one way to put in some operation signs to make these digits come to 100.
On my calculator I divided one whole number by another whole number and got the answer 3.125. If the numbers are both under 50, what are they?
Can you draw a square in which the perimeter is numerically equal to the area?
This multiplication uses each of the digits 0 - 9 once and once only. Using the information given, can you replace the stars in the calculation with figures?
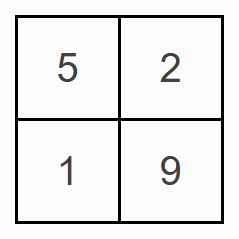
Choose four different digits from 1-9 and put one in each box so that the resulting four two-digit numbers add to a total of 100.
Can you make a cycle of pairs that add to make a square number using all the numbers in the box below, once and once only?
Use the interactivity to find all the different right-angled triangles you can make by just moving one corner of the starting triangle.
Find the product of the numbers on the routes from A to B. Which route has the smallest product? Which the largest?
Factor track is not a race but a game of skill. The idea is to go round the track in as few moves as possible, keeping to the rules.
My local DIY shop calculates the price of its windows according to the area of glass and the length of frame used. Can you work out how they arrived at these prices?
This challenge combines addition, multiplication, perseverance and even proof.
This task combines spatial awareness with addition and multiplication.
Use 4 four times in a calculation. What answers can you get?
Nine squares with side lengths 1, 4, 7, 8, 9, 10, 14, 15, and 18 cm can be fitted together to form a rectangle. What are the dimensions of the rectangle?
Can you order the digits from 1-3 to make a number which is divisible by 3 so when the last digit is removed it becomes a 2-figure number divisible by 2, and so on?
What is the largest 'ribbon square' you can make? And the smallest? How many different squares can you make altogether?
A game in which players take it in turns to choose a number. Can you block your opponent?
