This is part of our Secondary Curriculum collection of favourite rich tasks arranged by topic.
Scroll down to see the complete collection, or explore our subcollections on Perimeter and Area in two dimensions, and Surface Area and Volume in three dimensions.
problem
Favourite
Pair Products
Age
14 to 16
Challenge level
Choose four consecutive whole numbers. Multiply the first and last numbers together. Multiply the middle pair together. What do you notice?
problem
Favourite
Finding factors
Age
14 to 16
Challenge level
Can you find the hidden factors which multiply together to produce each quadratic expression?
problem
Favourite
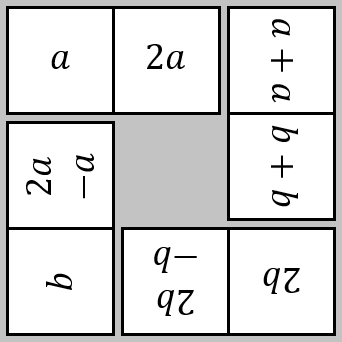
Factorising with Multilink
Age
14 to 16
Challenge level
Can you find out what is special about the dimensions of rectangles you can make with squares, sticks and units?
problem
Favourite
Hollow Squares
Age
14 to 16
Challenge level
Which armies can be arranged in hollow square fighting formations?
problem
Favourite
Perfectly Square
Age
14 to 16
Challenge level
The sums of the squares of three related numbers is also a perfect square - can you explain why?
problem
Favourite
Multiplication square
Age
14 to 16
Challenge level
Pick a square within a multiplication square and add the numbers on each diagonal. What do you notice?
problem
Favourite
Pythagoras Perimeters
Age
14 to 16
Challenge level
If you know the perimeter of a right angled triangle, what can you say about the area?
problem
Favourite
Difference of Two Squares
Age
14 to 16
Challenge level
What is special about the difference between squares of numbers adjacent to multiples of three?
problem
Favourite
Square Number Surprises
Age
14 to 16
Challenge level
There are unexpected discoveries to be made about square numbers...
problem
Favourite
Puzzling Place Value
Age
14 to 16
Challenge level
Can you explain what is going on in these puzzling number tricks?
problem
Favourite
Plus Minus
Age
14 to 16
Challenge level
Can you explain the surprising results Jo found when she calculated
the difference between square numbers?
problem
Favourite
What's Possible?
Age
14 to 16
Challenge level
Many numbers can be expressed as the difference of two perfect squares. What do you notice about the numbers you CANNOT make?
problem
Favourite
Why 24?
Age
14 to 16
Challenge level
Take any prime number greater than 3 , square it and subtract one. Working on the building blocks will help you to explain what is special about your results.
problem
Favourite
Always Perfect
Age
14 to 18
Challenge level
Show that if you add 1 to the product of four consecutive numbers the answer is ALWAYS a perfect square.
problem
Favourite
Harmonic Triangle
Age
14 to 16
Challenge level
Can you see how to build a harmonic triangle? Can you work out the next two rows?
problem
Favourite
2-Digit Square
Age
14 to 16
Challenge level
A 2-Digit number is squared. When this 2-digit number is reversed
and squared, the difference between the squares is also a square.
What is the 2-digit number?
Image
You may also be interested in this collection of activities from the STEM Learning website, that complement the NRICH activities above.