Our numbers
These spinners will give you the tens and unit digits of a number. Can you choose sets of numbers to collect so that you spin six numbers belonging to your sets in as few spins as possible?
Problem
For this activity I've chosen first of all to use a $1$ to $6$ and a $0$ to $9$ spinner.
The $1$ to $6$ we will use to give us the tens digit and the other one for the ones digit.
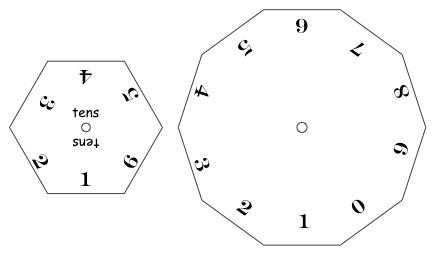
You will need two spinners like those above and two cards which each have six boxes drawn on them. You can download and print these, or you could use our interactive spinners. You will also need twelve counters.
A person with one card chooses the special types of numbers that they will collect. The other person chooses some other special types of numbers to collect.
For example, Sara chooses numbers you can share equally among $3$ ( eg. $3, 9, 21, 39 ... $).
Nala chooses even numbers (eg. $4, 10, 20, 44 ... $).
Each of them spins a spinner and then when it rests they read out the number (tens and ones).
Suppose it's a $21$, then Sara places a counter in one of the boxes on her card. If it is a $10$ then Nala gets a counter for her card. If it's a $30$ then both of them get a counter.
You can do something similar.
When you've tried it a few times decide what's best to choose so that you fill all the boxes on both cards as quickly as you can.
Spinners description
For accessibility. The link shows a sheet containing more spinners. The first spinner has numbers from 1 to 9. The second spinner has numbers from 1 to 8. The third spinner has numbers from 1 to 7. The fourth spinner has the numbers 1, 2, 3, 4, 1, 2, 3, 4.
Getting Started
What could you try first?
How will you know whether the spinners' number fits in your set?
Student Solutions
Jacob and James from Fishergate Primary School played this game using our interactive spinners.
Using spinners $1-6$ and $0-9$ we tried to see who would win if one was even and one was odd. The odds won as we got these numbers.
| Numbers |
| 25 |
| 32 |
| 29 |
| 35 |
| 54 |
| 52 |
| 55 |
| 22 |
| 35 |
| 51 |
| 11 |
Then we found out the $3$ times table beat the $5$ times table.
| Numbers |
| 29 |
| 51 |
| 22 |
| 36 |
| 26 |
| 51 |
| 11 |
| 54 |
| 23 |
| 26 |
| 37 |
| 10 |
| 69 |
| 24 |
Someone else wrote in to tell us that they found that broad sets work well if you have to get one but narrower sets work better if you want to get them all. Jacob and James then tried different spinners.
We did numbers more than $20$ and numbers less than $20$. Numbers more than $20$ won because there are four tens on the left spinner that would work but there are only two tens that would work for less than $20$.
| Numbers |
| 37 |
| 24 |
| 38 |
| 14 |
| 14 |
| 28 |
| 11 |
| 30 |
| 23 |
Teachers' Resources
Our Numbers
For this activity I've chosen first of all to use a $1$ to $6$ and a $0$ to $9$ spinner.
The $1$ to $6$ we will use to give us the "tens" figure and the other one for the "units" (or "ones").
Why do this problem?
Possible approach
Key questions
Possible extension
Possible support