Summing Consecutive Numbers

15 = 7 + 8 and 10 = 1 + 2 + 3 + 4. Can you say which numbers can be expressed as the sum of two or more consecutive integers?

Always the Same

Arrange the numbers 1 to 16 into a 4 by 4 array. Choose a number. Cross out the numbers on the same row and column. Repeat this process. Add up you four numbers. Why do they always add up to 34?

Fibs

The well known Fibonacci sequence is 1 ,1, 2, 3, 5, 8, 13, 21.... How many Fibonacci sequences can you find containing the number 196 as one of the terms?

Christmas Chocolates

Age 11 to 14
Challenge Level

Penny, Tom and Matthew were each given mint chocolates in a hexagonal box:

Penny ate $10$ chocolates and then quickly worked out that there must have been $61$ chocolates at the start.

Tom ate $20$ chocolates and then also managed to work out very quickly that there were originally $61$ chocolates:

Matthew ate $24$ chocolates and could also see very easily that he must have started with $61$ chocolates:

Can you see how each child managed to work out that there were $61$ chocolates in the full box?

You may find these chocolate box templates useful.

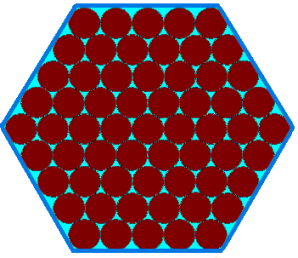
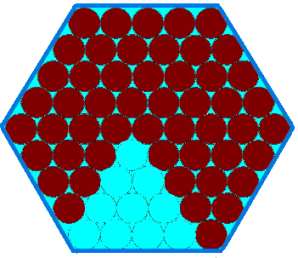
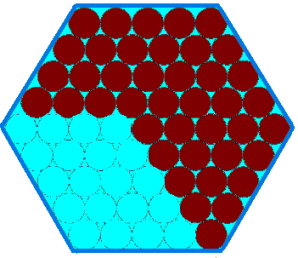
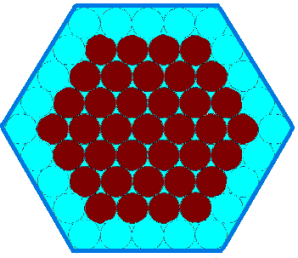
Penny, Tom and Matthew have been promised a larger box of chocolates as a Christmas present from their grandmother. The box will have $10$ chocolates along each edge, instead of just $5$.

How would each child work out how many chocolates the larger box will contain?
Can you describe any other ways to work it out?

Here are some more questions you might like to consider:

For which sizes of chocolate box will the three children be able to share the chocolates equally?
For which sizes of chocolate box will the boys be able to share the chocolates equally?
Can you describe how each child would work out the number of chocolates in a box with $n$ chocolates along each edge?

You may also like

Summing Consecutive Numbers

Always the Same

Fibs

Christmas Chocolates

Age 11 to 14Challenge Level

Age 11 to 14
Challenge Level