Farey Sequences
There are lots of ideas to explore in these sequences of ordered fractions.
Problem
Farey Sequences printable worksheet
If I gave you a list of decimals, you might find it quite straightforward to put them in order of size. But what about ordering fractions?
A man called John Farey investigated sequences of fractions in order of size - they are called Farey Sequences.
The third Farey Sequence, $F_3$, looks like this:
$$\frac01 \qquad \frac13 \qquad \frac12 \qquad \frac23 \qquad \frac11$$
It lists in order all the fractions between $0$ and $1$, in their simplest forms, with denominators up to and including $3$.
$F_4$ lists all the fractions between $0$ and $1$, in their simplest forms, with denominators up to and including $4$. Can you write it out? Click below to check once you've had a go.
Now that you've got the hang of it, write $F_5$.
Which extra fractions are in $F_5$ which weren't in $F_4$?
Which extra fractions will be in $F_6$ which aren't in $F_5$?
Where will they appear in the sequence?
There are lots of questions you could explore about Farey Sequences. Here are just a few that we thought of:
- How many extra fractions are there in $F_{11}$ that aren't in $F_{10}$?
- How many extra fractions are there in $F_{12}$ that aren't in $F_{11}$?
- Is every Farey Sequence longer than the one before? How do you know?
- Is there a way of working out how many fractions there will be in the next sequence?
- So far, all the Farey Sequences except $F_{1}$ have contained an odd number of fractions. Can you find a Farey Sequence with an even number of fractions?
Take some time to think about these and any other questions you decide to explore!
There is a curious link between the mediant of two fractions and Farey Sequences. See the problem Mediant Madness to learn more about mediants, and Farey Neighbours to apply it to Farey Sequences. Finally, the problem Ford Circles shows the relationship between these fractions and some beautiful geometrical patterns.
Getting Started
Here are all the fractions from the fifth Farey Sequence. They have been muddled up. Can you put them in order from smallest to largest?
Once you have put them in order, make a note of anything interesting you notice.
Student Solutions
Shriya from International School Frankfurt in Germany, Hayley and Yue from Colston's girls' school in the UK, Gabriel from Dulwich College Seoul, Ben and Henry from Robert Gordon's College in the UK, Antonio from International School of Luxembourg, Imran from Canada and Aadithya and Sivethini from Nower Hill High School in the UK found the new fractions in $F_5,$ $F_6,$ $F_{11}$ and $F_{12}.$ Ben said:
There are 4 fractions that appear in $F_5$ that don't appear in $F_4$. These are $\frac15, \frac25, \frac35$ and $\frac45.$
In $F_6,$ there are 2 new fractions that aren't in $F_5.$ These are $\frac16$ and $\frac56.$
These appear as these are the simplest forms of these fractions. In $F_{12}$ you couldn't have $\frac2{12},$ as that fraction can be and has been simplified into $\frac16.$
The new members of the sequences are the simplest form of each fraction.
Imran said:
- How many extra fractions are there in $F_{11}$ that aren't in $F_{10}$?
I found ten extra fractions. They are all the fractions that have the denominator as $11$ except $\frac0{11}$ and $\frac{11}{11}.$
- How many extra fractions are there in $F_{12}$ that aren't in $F_{11}$?
There are 4 extra fractions in $F_{12}$ that are not in $F_{11}.$ They are $\frac1{12},
\frac5{12}, \frac7{12},$ and $\frac{11}{12}.$
Is every Farey Sequence longer than the one before? How do you know?
Hayley, Gabriel, Shriya, Lucas from Powers Hall Academy in the UK, and Sivethini, Toby, Kanusha and Suahsini from Nower Hill High School in the UK claimed that every Farey sequence is longer than the one before. Gabriel said:
Every Farey sequence will be longer than the last because when the numerator is 1, there is no possible way to divide, consequently causing you not to be able to simplify the fraction. Therefore, because you can not simplify a fraction with a numerator of 1, you must add it [to the new Farey sequence].
Hayley noticed that as well as $\frac1n$, you always get $\frac{n-1}n$. This reminded Imran of something else:
We see that the numerators [denominators] of the first 2 and last 2 fractions correlate with the numbers in pascals triangle (other than $F_1$)!!! I found it really neat.
Is there a way of working out how many fractions there will be in the next sequence?
Yue, Scott, Timmy, Jayden & Charlie from Abingdon School in the UK, Shrish, Pritu and Harry from Bangkok Patana School in Thailand, Tamitha, Emma and Chanelle from Frederick Irwin Anglican School in Australia, and Sumayyah, Toby, Kanusha, Suahsini and Emer from Nower Hill noticed something about prime number Farey sequences. This is some of Tamitha, Emma and Chanelle's work:
Toby said this in a more general way:
When the number of a Farey sequence is prime it will have the number sequence it is minus 1 incremented from the previous sequence.
So if $p$ is prime, then $F_p$ has $p-1$ fractions that weren't in $F_{p-1}$.
Yue suggested a reason:
I think this happens because a prime number only has 2 factors (itself and 1)
Gabriel extended this to composite numbers:
If the denominator is not prime, add however many possible fractions there are but taking away how many can be simplified.
Shriya described a method:
The best way of working out how many fractions there will be in the next sequence is to first write down the new fractions [fractions with the new denominator]. Then you should cross out the fractions that have an equivalent fraction. Count the remaining fractions and add the number to the number of fractions the previous sequence has.
Scott, Timmy, Jayden & Charlie said something similar using a more formal notation:
(They mean that $A$ is the set of whole numbers up to $N$, $B$ is the numbers in $A$ which are not factors of $N$, and the number of new fractions is $n(B')$, which means the number of numbers that are in $A$ but not in $B$)
Scott, Timmy, Jayden & Charlie talk about factors, but actually this is not exactly right, because $\frac68$ can be simplified, even though $6$ is not a factor of $8$. In fact, we should be talking about something slightly different. Sumayyah, Kanusha, Emer and Shyam from Nower Hill used the term 'coprime'. This is Shyam's investigation into coprime numbers, and what their connection is to Farey sequences.

Sumayyah explained how this is related to what we've already seen:
Two consecutive numbers will always be coprime, so $\frac{x-1}x$ will always be added (e.g. $\frac45, \frac56, \frac78$)
Prime numbers will be co-prime with any number, so all numerators less than the denominator will be added to the sequence.
So far, all the Farey Sequences except $F_1$ have contained an odd number of fractions. Can you find a Farey Sequence with an even number of fractions?
Shrish, Pritu and Harry tried their best to find one, and decided that they couldn't. Click here to see their work.
Henry wrote a program which lists Farey sequences. Click below to see Henry's code.
t = 0
for i in range(len(lis)):
if lis[i][0]==elem:
t+=1
if t>0:
return True
else:
return False
def factorial(n):
v = 1
for i in range(1,n+1):
v = v*i
return v
def best(lis,n,ma):
final = []
lis2 = lis
for i in range(n):
x = 0
m = ma
for i in range(len(lis)):
if lis[i][0] < m:
x = i
m = lis[i][0]
final.append(lis2[x][1])
del lis2[x]
return final
def farey(n):
lis = []
v = factorial(n)
for i in range(n+1):
for j in range(1,i+1):
x = v*(j/i)
if not(contains(lis,x)):
lis.append([x,str(j),str(i)])
lis2 = []
for i in range(len(lis)):
lis2.append([lis[i][0],str(lis[i][1])+"/"+str(lis[i][2])])
return best(lis2,len(lis2),2*v)
print(farey(25))
Additionally, print(len(farey(25)) will tell you how many fractions are in the Farey sequence. Note that 0 is not included, so they are all even numbers now!
Lilly from Frederick Irwin, and Sumayyah, Leo, Aadithya, Sivethini, Kanusha, Emer and Suahsini from Nower Hill, Henry and Shriya noticed some symmetry in the Farey sequences which can help explain why they contain odd numbers of fractions. Lilly said:
I found that the fractions were mirrored and that each time there was a new sequence, it was adding on two fractions at a time.
Aadithya said:
Sumayyah drew a diagram showing the fractions around a circle, which shows the symmetry. Click here to see Sumayyah's diagram.
In fact, the reason for this symmetry is that if $a$ and $n$ are coprime, $n-a$ and $n$ are also coprime. Click below to see a short proof of this.
Imagine that $n-a$ and $n$ are not coprime, so they are both in the $c$ times table for some number $c$.
But the difference between two numbers in the $c$ times table is always a multiple of $c$.
So the difference between $n-a$ and $n$, which is $a$, is a multiple of $c$.
But then $a$ and $n$ are both multiples of $c$, so they are not coprime!
So if $n-a$ and $n$ are not coprime, then $a$ and $n$ are not coprime either. So if $a$ and $n$ are coprime, then $n-a$ and $n$ must be coprime too.
We are delighted that some students sent in solutions that explored Farey sequences even further. Below are further investigations into the number of fractions in each sequence, and into the mediants (as introduced in Mediant Madness, the mediant of $\frac ab$ and $\frac cd$ is $\frac{a+b}{c+d}$), sums and means of fractions in Farey sequences.
The number of fractions in each sequence
Imran and Lucas made an interesting observation about the number of fractions in the first few Farey sequences. Imran said:
I wrote the number of fractions in each sequence below:
$F_1\rightarrow2$
$F_2\rightarrow3$
$F_3\rightarrow5$
$F_4\rightarrow7$
$F_5\rightarrow11$
$F_6\rightarrow13$
We can see that there is a pattern of consecutive prime numbers.
Therefore, all we have to do is to find the prime number belonging to $F_n$ and we know the number of fractions! :-) Since there is no definite formula for finding the $n$th prime number there is also no way to calculate number of fractions in the sequence $F_n.$
However, this pattern doesn't continue. Aadithya found:
$F_7\rightarrow19$
$F_8\rightarrow23$
$F_9\rightarrow29$
$F_{10}\rightarrow33$ (which is not prime)
Leo and Suahsini examined the differences between the number of terms in each Farey sequence, and the difference between the differences, and so on. Leo claimed to have found a very nice pattern, but unforunately had a small mistake. This is Suahsini's work, which did not identify a pattern:
Markus plotted these differences:
I decided to plot the [number of values] added in a bar chart, with the $y$ axis being number of values [added] and the $x$ axis being the Farey sequence number.
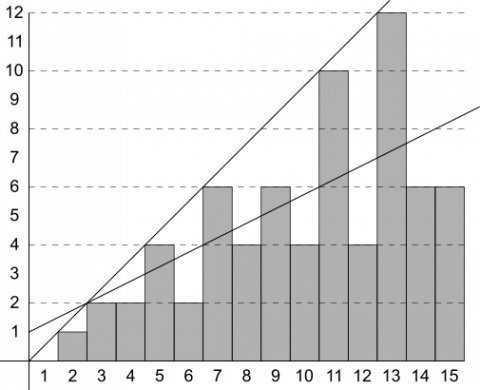
This led to two [lines], one for prime numbers, the other for other numbers. The one for all numbers is $y=\frac12x+1$.
It is true that the line connecting the bars of the prime numbers continues to connect the bars of all of the prime numbers. Can you explain why?
Markus' line $y=\frac12x+1$ doesn't actually touch any more of the bars. Can you explain why?
Henry mentioned a special function:
The number of fractions in $F_n$ that are not in $F_{n-1}$ is always $\phi(n)$ - the Euler totient of $n$. Thus:
$|F(n)| =1+ \phi(1) + \phi(2)+...\phi(n)$
The Euler totient function, $\phi(n)$, is usually defined as: $\phi(n) = \text{the number of numbers less than }n\text{ that are coprime to }n$.
It could equivalently be defined as: $\phi(n) = \text{the number of fractions that appear in }F_n\text{ that are not in }F_{n-1}$.
Sumayyah, Manav, Kanusha, Markus, Emer and Suahsini also investigated the mediant of the fractions in the Farey sequences, as introduced in Mediant Madness. This is Emer's work, which is also about the median and the mean:
Sivethini and Suahsini also found this result for the mean, but Sivethini described it in a different way:
The sum of the fractions in a Farey sequence multiplied by 2 equals the total number of values in that sequence.
Finally, Manav from Nower Hill investigated mediants much further. This is Manav's work:
Teachers' Resources
Why do this problem?
Ordering fractions can seem like quite a mundane and routine task. This problem encourages students to take a fresh look at the process of comparing fractions, and offers lots of opportunities to practise manipulating fractions in an engaging context where students can pose questions and make conjectures.
Possible approach
This printable worksheet may be useful: Farey Sequences
$$\frac01 \qquad \frac11$$ $$\frac01 \qquad \frac12 \qquad \frac11$$ $$\frac01 \qquad \frac13 \qquad \frac12 \qquad \frac23 \qquad \frac11$$
Give students a short time to look at the sequences on their own, and then encourage them to discuss with their partners. Then bring the class together and share ideas. Clarify that a Farey sequence contains all the fractions with a denominator up to a particular number, in their simplest form, in order, and write up $F_4$ on the board: $$\frac01 \qquad \frac14 \qquad \frac13 \qquad \frac12 \qquad \frac23 \qquad \frac34 \qquad \frac11$$
This is a good opportunity to clarify the rule about equivalent fractions by asking "Where is $\frac{2}{4}$?"
- How many extra fractions are there in $F_{11}$ that aren't in $F_{10}$?
- How many extra fractions are there in $F_{12}$ that aren't in $F_{11}$?
- Is every Farey Sequence longer than the one before? How do you know?
- Is there a way of working out how many fractions there will be in the next sequence?
- So far, all the Farey Sequences except $F_{1}$ have contained an odd number of fractions. Can you find a Farey Sequence with an even number of fractions?
Key questions
If $\frac1n<\frac1m$ what can you say about $n$ and $m$?
Why is each Farey Sequence longer than the last?
When does a Farey Sequence have lots of extra entries?
When does it have only a few?
When is $\frac{a}{b}< \frac{c}{d}$?
Possible support
Tumbling Down uses fraction walls to provide a possible route into understanding Farey Sequences.
