Surprising Equalities
Take any triangle, and construct squares on each of its sides. What do you notice about the areas of the new triangles formed?
Problem
For this problem, you might like to use dynamic geometry software such as GeoGebra, which is free to download and use. If you have never used GeoGebra before, you might like to read this article first.

Draw any triangle $ABC$ and construct squares on each of its sides.
Join the vertices of the squares as shown in the diagram to create three more triangles.
Work out the area of the four triangles.
What do you notice?
Can you prove it?
Take a look at the Getting Started section to explore some interactive diagrams, or click below to see an image together with some questions which might help you to construct a proof.

What transformation takes the point E to the point E'?
How does triangle ACE' relate to triangle ADE?
What proportion of triangle BCE' is triangle ABC?
Can you rotate the other grey triangles in a similar way?

Here is a similar picture, which shows a quadrilateral $ABCD$ with a square constructed on each of its edges.
Triangles, which have been shaded, have been constructed between the squares.
Use your previous result to show that the areas of opposite triangles sum to the area of the quadrilateral $ABCD$.

Finally, this picture is constructed around an unremarkable triangle, with two arbitrary squares constructed on one edge.
Single squares are then constructed on each of the remaining edges of the triangle.
Triangles are then drawn between the squares as shown.
Use your previous results to prove that the area of the darker shaded triangle $CIL$ is equal to the sum of the areas of the other two triangles $AKF$ and $BGJ$.
Getting Started
The GeoGebra interactivities below may be useful for exploring the problem.
What do you notice about the areas of the four triangles as you change the original triangle?
Use the slider to rotate the three outer triangles through $90^{\circ}$. Can you come up with a convincing argument to explain why each triangle has the same area as the original triangle?
Student Solutions
Mathula from Doha College in Qatar made some observations using GeoGebra. Mathula's work below includes finding the areas manually using the cosine rule
($a^2 = b^2 + c^2 - 2bc\cos A$) and the formula for the area of a triangle $A=\frac12 ab\sin C$.
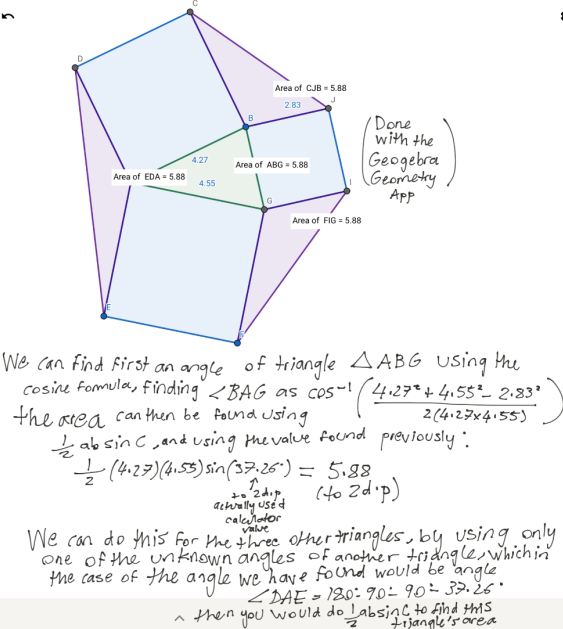
Beste from Turkey, Max, Ashwin, Jayden and Will and Jakob and Scott from Abingdon School in the UK and Mathula all proved that the four triangles have the same area using these two rules. This is Jakob and Scott's work:
This is Mathula's explanation of step 5:

The sine wave has an axis of symmetry at 90, as $\sin{0}$ and $\sin{180}$ have the same value.
The red text says:
these points are equidistant from the line of symmetry, which means they are equidistant from $0$ and $180$
if one of these points is $x$, the other point is $(90-x)+90=180-x$ AND THEY HAVE THE SAME $\sin x$ VALUE
There is another method which the second interactivity in the Getting Started section can help you find.
Click to see the solution using this method.

The areas of each of the four triangles are the same. We can show this for triangles $ABC$ and $ADE$ by rotating the triangle $ADE$ through $90^{\circ}$ anticlockwise, so that $AD$ lies along $AC$ (the blue shaded triangle). Then $AB=AE'$, so $AC$ is a median of the triangle $BCE'$. Hence triangle $ABC$ has the same area as triangle $ACE'$ and therefore also the triangle $ADE$. (Or we can just notice that $BA=AE'$ and triangles $ABC$ and $ACE'$ have the same perpendicular height).
Beste and Max, Ashwin, Jayden and Will and Mathula used their result about the triangle to prove similar results about the quadrilateral and the triangle with two squares on one side. This is Beste's work on the quadrilateral:
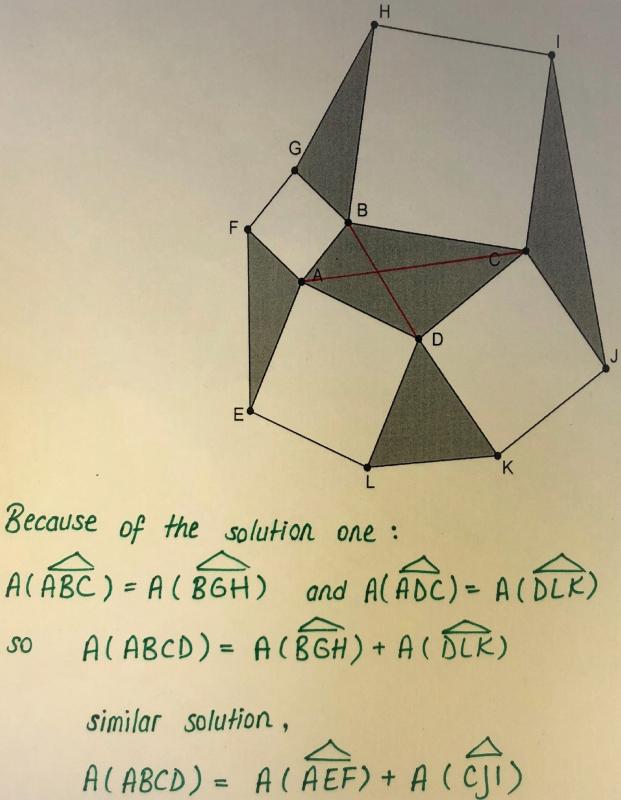
This Max, Ashwin, Jayden and Will's work on the triangle with two squares on one side, with Beste's diagram.

Triangle ABC = triangle CIL - as proven in part 1
Draw a line between C and D.
Triangle ACD = triangle AFK
Triangle BCD = triangle BGJ
Therefore, ABC = AFK + BGJ
Therefore, CIL = AFK + BGJ
Teachers' Resources
Why do this problem?
This problem presents students with a surprising result which we hope they will want to explain. By using dynamic geometry, students can see that the triangles appear to have the same area regardless of the starting configuration, but to provide a convincing explanation and proof will require some determination and resilience.
As well as the proof suggested in the hint, it is possible to prove the result using trigonometric formulae, so the problem is a great opportunity to consolidate work on different areas of the geometry curriculum as well as appreciating the elegance of a variety of solution methods.
Possible approach
Students could begin by drawing triangles on dotty paper and then constructing the squares on the sides like those created in Tilted Squares. Then they could work out the areas of the triangles using Pick's Theorem. They may then wish to move on to using GeoGebra to see if any relationships they notice still hold for the many cases they can generate dynamically.
The article Using Digital Manipulatives and Interactivities to Develop Curiosity emphasises the importance of proof when using dynamic geometry; students should not be satisfied by seeing the areas stay the same in the software, as there could be rounding errors. We can't be sure that the areas are always equal unless we prove it!
In the Getting Started section, there is an interactive GeoGebra applet which shows the outer triangles rotating to line up with the original triangle. This, together with the diagram in the problem and the supporting questions, can be used to help students work towards a proof. Alternatively, students who have met the formula $\frac12ab \sin C$ for the area of a triangle could be encouraged to use this, together with their understanding of the relationship between $\sin \theta$ and $\sin (180-\theta)$, to construct a proof.
The two follow-up problems offer a good opportunity for students to adapt their thinking from the first part of the problem and apply it to a new situation.
Key questions
Does it help to add any new lines, or to rotate part of the diagram?
If I knew the sides and the angles, how would I work out the area of the triangle?
How are the angles of the original triangle and the new triangles related?
Possible extension
Students could try Areas and Ratios, which explores idea of areas of triangles with a shared vertex further.
Possible support
Triangle in a Triangle might provide a useful warm-up to get students thinking about methods of geometrical proof.
