Areas and ratios
Do you have enough information to work out the area of the shaded quadrilateral?
Problem
Areas and Ratios printable sheet - with clues
Areas and Ratios printable sheet - without clues
In the diagram below (which is not drawn to scale), the area of the three triangular regions is given.
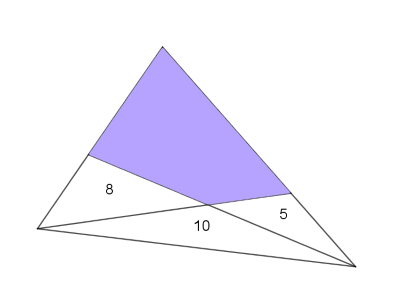
Can you work out the area of the shaded quadrilateral?
Perhaps it feels as though there isn't enough information to solve this problem!
If you are stuck, click below to reveal some suggestions that may help you.
First suggestion:
In the GeoGebra applet below, you can move the dots to create different triangles with bases which lie on the same straight line and with a shared apex.
What is the relationship between the ratio of the two areas and the ratio of the two lengths?Can you explain why?
Can you apply this to the original problem?
Second suggestion:
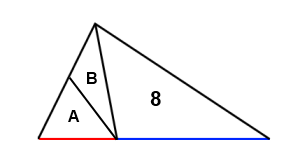
The red line is half the length of the blue line. Numbers and letters inside a triangle represent its area. What can you say about $A+B$?
Third suggestion:
It might be useful to label the points in the diagram. You could also split the quadrilateral into two triangles, and label them:
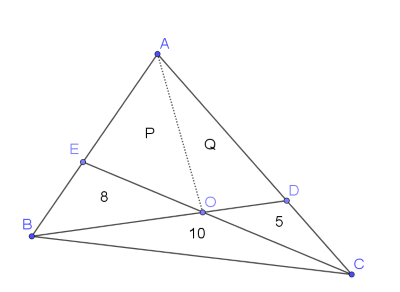
Can you use the ideas from the first two suggestions to write down some relationships in terms of P and Q?
Getting Started
What happens to the area of a triangle if I keep the height the same but double the base? Or treble it? Or...?
Student Solutions
Reyna from Downside School, Jian from NLCS Jeju in South Korea and Kian from King Edward VII School in the UK all found the area of the quadrilateral using ratios. They all used the result below, which Kian and Jian both proved. This is Jian's proof:
Jian, Kian and Reyna used this idea to find the area of the quadrilateral. This is Reyna's working:


Jack used a different method:
The problem is best solved considering the similar triangles made from drawing a line parallel to the base through the cross of the two diagonals.
I found the ratio of the heights of the combined triangles of area $15$ and $18$ and the triangle of area $10.$
Then Jack used the fact that the triangles on the line parallel to the base are similar to those on the base, so their areas can be found by multiplying by the squares of the scale factors:
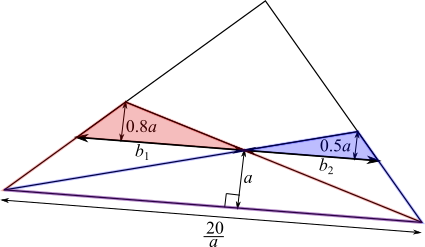
$\left(\dfrac{0.8}{1.8}\right)^2\times18=\dfrac{6.4}{1.8}=\dfrac{32}9$
$ \left(\dfrac{0.5}{1.5}\right)^2\times15=\dfrac{15}{9}=\dfrac{5}3$
$\dfrac{32}9=\dfrac120.8ab_1\Rightarrow b_1=\dfrac{80}{9a}$
$\dfrac{5}3=\dfrac120.8ab_2\Rightarrow b_2=\dfrac{20}{3a}=\dfrac{60}{9a}$
After solving for their area I was able to find the width of the triangle at that height
($b_1+b_2$) and used ratios to find the height of the triangle.
$b_1+b_2=\dfrac{140}{9a}$
$h=4.5a$ (going up $a$ units along the height, the base gets shorter by $\frac{40}{9a}$ units. The base is $\dfrac{20}a$, and $\dfrac{20}a\div\dfrac{40}{9a}=4.5$. So after going up $a$ units $4.5$ times, the 'base' has reached $0$ - so we are at the point of the triangle)
I then obtained an area of $45-23=22$ for the quadrilateral.
Teachers' Resources
Why do this problem?
This problem presents a geometrical situation where it appears there is not enough information to solve the problem. However, by persevering and making use of the hints given in the task, students will be surprised to discover that an elegant solution can be found.
Possible approach
Begin by sharing this image and invite students to suggest a lower and upper bound for the shaded area.

"Do you think we have enough information to work out the area exactly?"
Give students some time to think about what they know and what they can work out. They may conclude that there's not enough information.
"Sometimes we can get insights from looking at a simpler problem first..."
Share the interactive GeoGebra applet from the problem and invite students to suggest and explain a relationship between the bases and the areas of the triangles. Then refer back to the original problem - "Are there any relationships between lengths that we can deduce?"
"Another useful tool for solving geometry problems is to label our diagram to make it easier to talk about, and add in extra lines..."
Show this image:

"Can you find expressions which include P and Q based on what we know about areas and lengths? Does this help us to solve the problem?"
Finally, encourage students to write up their solution formally, making sure that they justify each step of the method clearly.
Key questions
What do we know?
What can we deduce?
If $O$ lies on $BD$, and $BOC$ has twice the area of $DOC$, what can we say about the lengths $BO$ and $OD$?
What does this tell us about areas $BOA$ and $AOD$?
Possible support
Students could start by exploring Triangle in a Triangle.
Possible extension
Another Triangle in a Triangle provides a suitable follow-up challenge that uses similar ideas.
