Are We Nearly There?
Can you describe the route followed by the arrows?
Problem
Route to Infinity is a more recent version of this problem
This resource is part of "Dotty Grids - Exploring Coordinates and Vectors"
Image
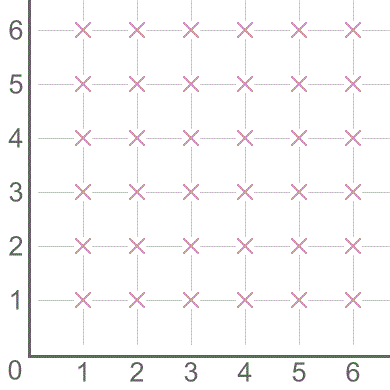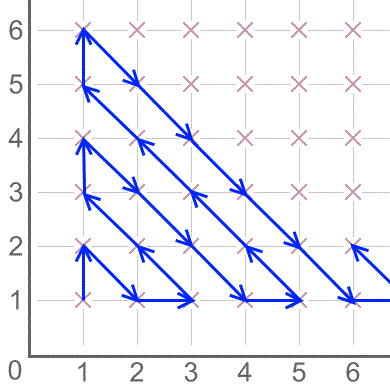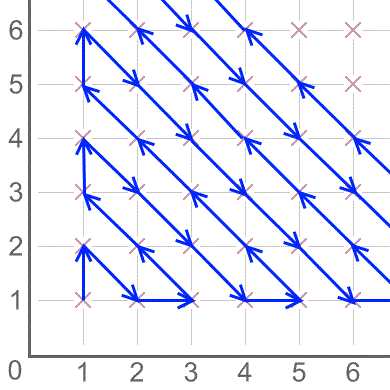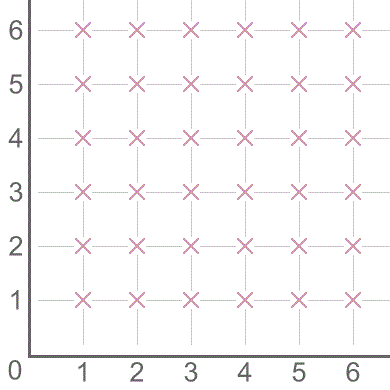
Take some time to look at the route followed by the arrows in this diagram.
Can you now look away and list the points visited?
If the pattern of arrows continues for ever, which point will be the $100^{th}$ to be visited?
How many steps will it take to reach (60,40)?
Where will the next step take you to?
Can you design an alternative route that visits all the points on a grid?
Can you still work out how many steps it will take you to reach (60,40)?
Getting Started
Student Solutions
Thank you to everyone who submitted solutions to this problem. There were lots of good solutions; well done!
Ollie and Ziggy, from Priestlands School, made this observation:
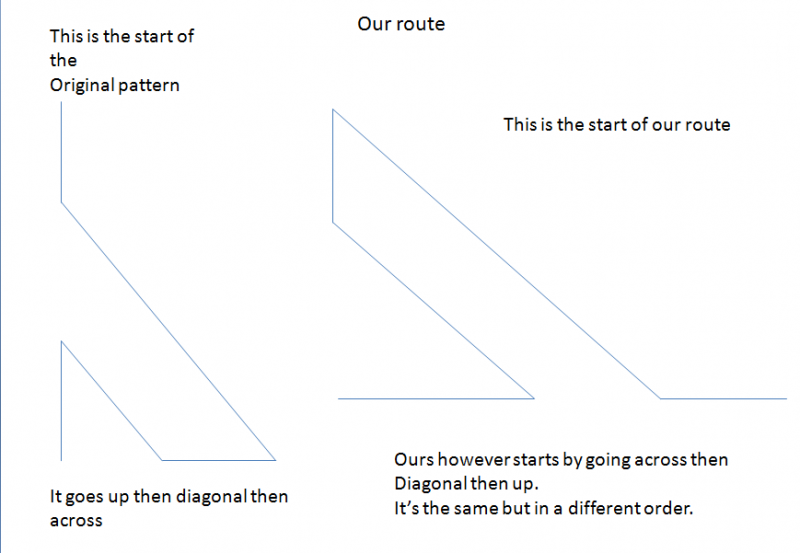
The line goes: up 1 step, diagonally 1 step, across 1 step, diagonally 2 steps, and so on.
Each new diagonal line is 1 step longer than the last diagonal line.
Matt, Tom and Ollie, also from Priestlands School, were able to tell us how to work out the number of points in the previous rows.
The lengths of the diagonals can be found by adding $1+2+3+4+5+...$, ending at the length of the final diagonal.
These sums are also known as the triangle numbers.
Sunny, from Carmel Pak U Secondary School, Hong Kong, and Phil, from Our Lady of Lourdes School, Canada were able to use this to find the coordinates of 100. Here is Sunny's solution:
Image
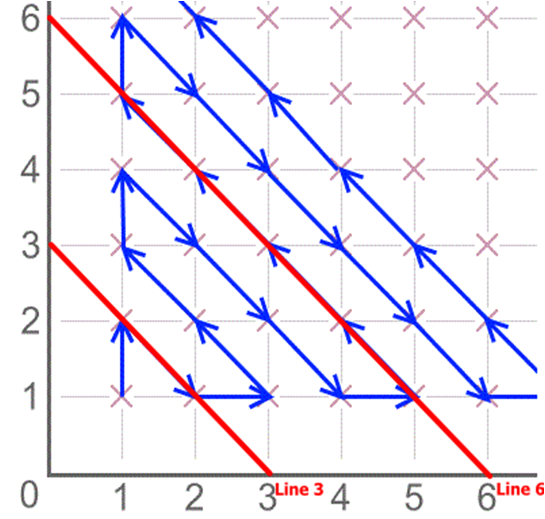
Looking at the 15th line, this has $1+2+3+4+5+6+7+8+9+10+11+12+13+14 = 105$, so we are ahead by $5$ dots.
Since line three goes down, line 4 goes up and in general the even lines go up and the odd lines go down, the line is going down.
Therefore: $105$ is at $(14,1)$.
$104$ is at $(13,2)$
$103$ is at $(12,3)$
$102$ is at $(11,4)$
$101$ is at $(10,5)$
$100$ is at $(9,6)$
Sunny then went on to describe how to find the number at $(60,40)$.
Since $60+40=100$, $(60,40)$ is on line $100$, so the final number on this diagonal is $4950$, as this is $1+2+3+4+...+98+99$.
Since $100$ is even, this line is going up, so we need to go back $59$ steps to get back to $(60,40)$.
This means the number is $4950 - 59 = 4891$.
Ziggy and Ollie found an alternative route that visited all the numbers:
Image
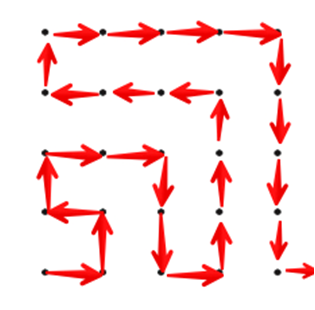
Sunny found a different alternative route:
Image
Image

Image

Image

Hannah went on to describe the same alternative path as Sunny. She was also able to say how long it would take to reach $(60,40)$ on this path.
Image
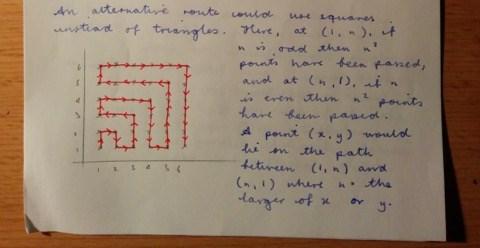
Image

Hannah also made an excellent observation about her two paths, which she could use to connect square and triangle numbers. She used algebra to prove that this relationship would always work.
Image

Image

This reminded me of Picturing Triangle Numbers, which you might want to take a look at.
Well done and thank you to everyone who submitted solutions.
Teachers' Resources
For ideas on how this problem and others from the Dotty Grids Collections can be used in the classroom, you may be interested to read this article.
Here is a poster version of this problem that you may wish to print out and use.
