Picturing Triangular Numbers

Triangular numbers can be represented by a triangular array of squares.

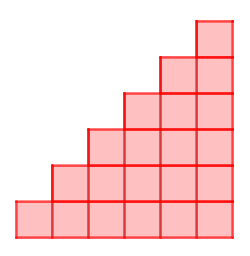
Imagine two copies of a triangular array of squares. Can you picture how to fit them together to make a rectangle? What is special about the dimensions of your rectangle?

Use the activity below to test your ideas.

What do you notice about doubling triangular numbers?
Experiment with different triangle numbers and explain what is special about the rectangles made from two identical triangle numbers.

Can you write down the dimensions of the rectangle made from two copies of the 250th triangle number? Can you use this to work out the 250th triangle number?

Check - your answer should be somewhere in this list:
29184, 31375, 586594, 908475, 2092035

Deduce a strategy for working out any triangle number.

 

 

Extension:

Consider the following numbers: $4851, 6214, 3655, 7626, 8656$.

Which are triangle numbers?
How did you decide?

Do any triangle numbers end $000$?

 

 

You may wish to try the problems Mystic Rose and Handshakes. Can you see why we chose to publish these three problems together?

 

You may also be interested in reading the article Clever Carl, the story of a young mathematician who came up with an efficient method for adding lots of consecutive numbers.