Dotty Grids in the Classroom

Age 11 to 18

Article by Charlie Gilderdale and Alison Kiddle

Published 2014

In our latest feature, we have chosen the environment of a dotty grid and put together some starting points to encourage students to explore and discover some mathematical ideas.

Starting with a blank dotty grid, students begin by simply drawing squares. This can provoke thoughts about properties of squares, and can lead to important insights involving coordinates and vectors. Exploring diagonals of squares and rhombuses can lead to generalisations that can be proved geometrically or using vectors.

We invite students to consider area. After a period of exploration, they may discover results such as Pick's theorem and Pythagoras's theorem, while getting plenty of practice at finding areas.

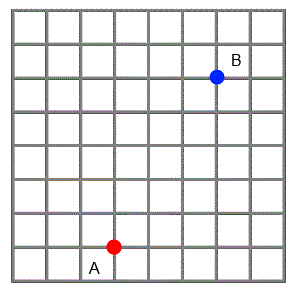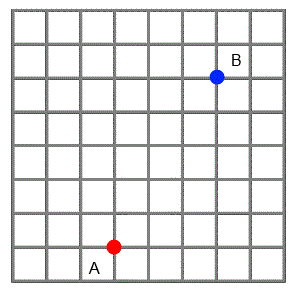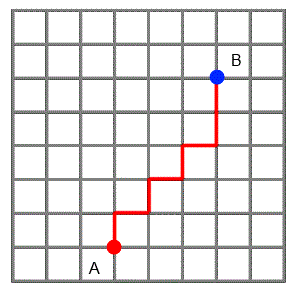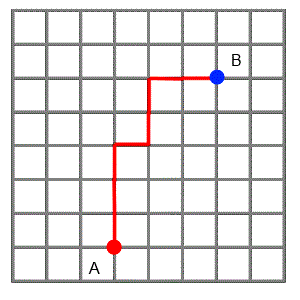
Students can explore distance on dotty grids, using taxi-cab geometry. A simple starting point about how to get from A to B can lead to a wide variety of interesting mathematical questions. Pascal's Triangle and the Binomial Theorem might even crop up!

These starting points capture our "Low Threshold High Ceiling" philosophy. The starting points offer investigative opportunities that are accessible to a wide range of students. These can prompt conjectures, generalisations, justification and proof as well as more advanced mathematical content.

The resources offer an informal and unstructured approach for students to work on individually and make discoveries for themselves and at their own pace. To see how you could use these starting points in the classroom to encourage collaborative learning and problem solving, take a look at these videos showing how two members of the NRICH team worked with a group of students in a structured lesson on finding areas of squares. Other starting points can be used in the classroom in a similar way. We would be delighted to hear from teachers who wish to share their stories about how these starting points can lead to multiple discoveries.

To support exploration on dotty grids, we have developed an interactive dotty grids environment. The interactive tool records not just the finished drawing but also how it was made, so it can be used for students to record and share the development of their thinking. There is a "share" button to allow students to send us their drawings together with their ideas. Of course, you can also print out dotty grids for students to work on with pencil and ruler, and share pictures of their work with us. We have also used GeoGebra in some of the starting points, so students might find it useful - it is free to download.

We hope you and your students will share ideas beyond your own classroom and contribute to a worldwide community of young mathematicians through the NRICH site! We'd welcome any interesting ideas, alternative starting points, discoveries, conjectures, generalisations, justifications or proofs that students wish to send us.