Enlargements and scale factors

problem
Favourite

Poly Plug Pattern

Age

5 to 7

Challenge level

1 out of 3

Create a pattern on the small grid. How could you extend your pattern on the larger grid?
problem
Favourite

Hex

Age

11 to 14

Challenge level

1 out of 3

Explain how the thirteen pieces making up the regular hexagon shown in the diagram can be re-assembled to form three smaller regular hexagons congruent to each other.
problem
Favourite

Growing Rectangles

Age

11 to 14

Challenge level

1 out of 3

What happens to the area and volume of 2D and 3D shapes when you enlarge them?
game
Favourite

Transformation Game

Age

11 to 14

Challenge level

2 out of 3

Why not challenge a friend to play this transformation game?
$Who \is the \fairest of \them \all ?$

problem
Favourite

Who Is the Fairest of Them All?

Age

11 to 14

Challenge level

3 out of 3

Explore the effect of combining enlargements.
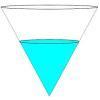
problem
Favourite

Fill Me Up Too

Age

14 to 16

Challenge level

2 out of 3

In Fill Me Up we invited you to sketch graphs as vessels are filled with water. Can you work out the equations of the graphs?
problem
Favourite

Squirty

Age

14 to 16

Challenge level

3 out of 3

Using a ruler, pencil and compasses only, it is possible to construct a square inside any triangle so that all four vertices touch the sides of the triangle.
problem
Favourite

Fit for Photocopying

Age

14 to 16

Challenge level

3 out of 3

Explore the relationships between different paper sizes.
problem
Favourite

Circles Ad Infinitum

Age

16 to 18

Challenge level

2 out of 3

A circle is inscribed in an equilateral triangle. Smaller circles touch it and the sides of the triangle, the process continuing indefinitely. What is the sum of the areas of all the circles?
problem

Arrow Arithmetic 1

Age

14 to 16

Challenge level

1 out of 3

The first part of an investigation into how to represent numbers using geometric transformations that ultimately leads us to discover numbers not on the number line.