Hex
Problem
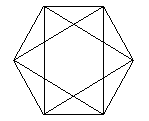
Explain how the thirteen pieces making up the regular hexagon shown in the diagram can be re-assembled to form three smaller regular hexagons congruent to each other.
Click here for a poster of this problem.
Getting Started
Student Solutions
Malcolm Findlay from Madras College in St Andrews, Scotland has solved the first part of this problem:
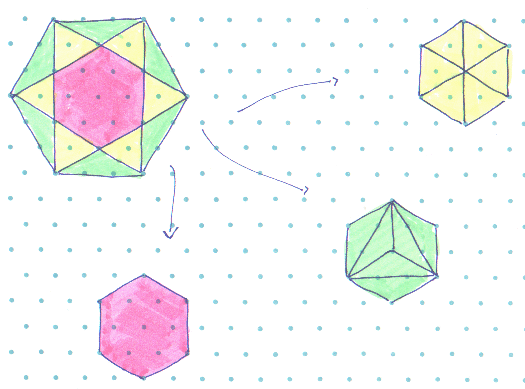
Izumi Tomioka, Carol Chow and Priscilla Luk from The Mount School in York solved the second part of the problem:
The original hexagon has sides of length 3 units and we need to work out $x$, the lengths of the sides of the smaller hexagons.
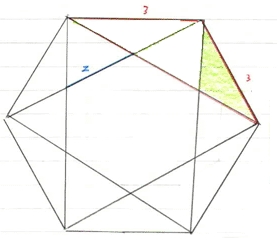
The hexagon below has been made from 6 of the shaded triangles
above.
We need to find the length of one of the sides of this hexagon.
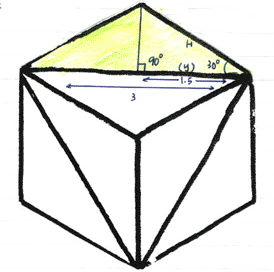
Splitting the shaded triangle into half gives us a right angled triangle such that: $$\cos30 = {1.5\over H}$$ $$H = {1.5\over \cos 30}$$ $$H = 1.73$$
Andrei Lazanu (aged 12) from School 205 in Bucharest, Romania, solved both parts of the problem.
This is how he tackled the second part:
To calculate the lengths of the sides of the smaller hexagons I used the following notations:
l for the length of side of the great hexagon
a for the length of side of the small hexagon
I used the following notation:
Triangle ACE is equilateral, because its sides are
congruent.
So, angle EAC is $60$ °.
Angle FAB is $120$ °, since each angle of a regular hexagon is $120$ °.
Triangle AEF is congruent with triangle ACB, having all sides
congruent. They are also isosceles triangles.
This means that each of the angles FAE and CAB is
$30$ °.
Therefore angle EAB is $90$ °.
Triangle AMN is also equilateral, because it has a
$60$ ° angle (MAN) and AM = AN.
Triangle ANB is isosceles, so AN and NB are congruent.
Therefore, in the right angled triangle MAB,
MA = MN = NB = $a$
AB has length $l$
Applying the Pythagorean Theorem: $$l^2 = (a + a)^2 - a^2$$ $$l^2 = 4a^2 - a^2$$ $$l^2 = 3a^2$$ $$l = a \sqrt{3}$$
If the length of the side of the great hexagon is 3 units long $l = 3$
Therefore $a = \sqrt{3}$ units
An alternative way of calculating "a" takes into account the
first part of the problem:
the area of the great hexagon is three times the area of the small
one.
For a hexagon of side $l$, the area is calculated as 6 times the
area of an equilateral triangle of side $l$,
this means that the area of the great hexagon is:
| $6{l^2 \sqrt3\over 4} = {l^2 3\sqrt3\over2}$ | $ | (1)$ |
The 3 smaller hexagons of side "a" have a total area of:
| $3{a^2 3\sqrt3\over 2} = {a^2 9\sqrt3\over2}$ | $(2)$ |
Since, $(1)$ and $(2)$ represent the same area, $3a^2 = l$
which is the same as we found above.
