problem
Reach 100
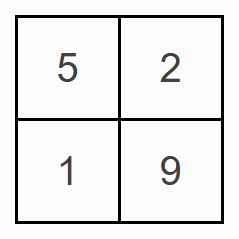
Choose four different digits from 1-9 and put one in each box so that the resulting four two-digit numbers add to a total of 100.

Choose four different digits from 1-9 and put one in each box so that the resulting four two-digit numbers add to a total of 100.

Can you make square numbers by adding two prime numbers together?
What is the total area of the four outside triangles which are outlined in red in this arrangement of squares inside each other?
What do the numbers shaded in blue on this hundred square have in common? What do you notice about the pink numbers? How about the shaded numbers in the other squares?