Tessellations

article
Shaping Up With Tessellations

This article describes the scope for practical exploration of tessellations both in and out of the classroom. It seems a golden opportunity to link art with maths, allowing the creative side of your children to take over.
article
Creative Approaches to Mathematics Across the Curriculum

Suggestions for teachers about exploring maths in different contexts: art, history and so on
article
Outside the Box

This article explores the links between maths, art and history, and suggests investigations that are enjoyable as well as challenging.
page
Lafayette

What mathematical words can be used to describe this floor covering? How many different shapes can you see inside this photograph?
page
Making Maths: Kites and Darts

Using these kite and dart templates, you could try to recreate part of Penrose's famous tessellation or design one yourself.
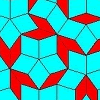
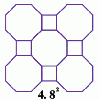problem

Schlafli Tessellations

Age

11 to 18

Challenge level

are somewhat mundane they do pose a demanding challenge in terms of 'elegant' LOGO procedures. This problem considers the eight semi-regular tessellations which pose a demanding challenge in terms of 'elegant' LOGO procedures.
problem

Triominoes

Age

11 to 14

Challenge level

A triomino is a flat L shape made from 3 square tiles. A chess board is marked into squares the same size as the tiles and just one square, anywhere on the board, is coloured red. Can you cover the board with trionimoes so that only the square is exposed?
problem

Tessellating Hexagons

Age

11 to 14

Challenge level

Which hexagons tessellate?
problem
Favourite

Cover the Camel

Age

5 to 7

Challenge level

Can you cover the camel with these pieces?
problem
Favourite

Repeating Patterns

Age

5 to 7

Challenge level

Try continuing these patterns made from triangles. Can you create your own repeating pattern?