Reasoning, convincing and proving
-

-
 problem
problemSixational
The nth term of a sequence is given by the formula n^3 + 11n. Find the first four terms of the sequence given by this formula and the first term of the sequence which is bigger than one million. Prove that all terms of the sequence are divisible by 6. -
 problem
problemBig, bigger, biggest
Which is the biggest and which the smallest of $2000^{2002}, 2001^{2001} \text{and } 2002^{2000}$?
-
 problem
problemA biggy
Find the smallest positive integer N such that N/2 is a perfect cube, N/3 is a perfect fifth power and N/5 is a perfect seventh power. -
 problem
problemFitting in
The largest square which fits into a circle is ABCD and EFGH is a square with G and H on the line CD and E and F on the circumference of the circle. Show that AB = 5EF. Similarly the largest equilateral triangle which fits into a circle is LMN and PQR is an equilateral triangle with P and Q on the line LM and R on the circumference of the circle. Show that LM = 3PQ -
 problem
problemConverse
Clearly if a, b and c are the lengths of the sides of an equilateral triangle then a^2 + b^2 + c^2 = ab + bc + ca. Is the converse true? -
 problem
problemThree ways
If x + y = -1 find the largest value of xy by coordinate geometry, by calculus and by algebra. -
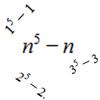 problem
problemCommon divisor
Find the largest integer which divides every member of the following sequence: 1^5-1, 2^5-2, 3^5-3, ... n^5-n. -
 problem
problemLong short
What can you say about the lengths of the sides of a quadrilateral whose vertices are on a unit circle? -

