Reasoning, convincing and proving

problem
Thousands and millions

Age

11 to 14

Challenge level

Here's a chance to work with large numbers...
problem
Reaction timer

Age

11 to 14

Challenge level

This problem offers you two ways to test reactions - use them to investigate your ideas about speeds of reaction.
problem
LCM Sudoku

Age

14 to 16

Challenge level

Here is a Sudoku with a difference! Use information about lowest common multiples to help you solve it.
problem
All in a jumble

Age

11 to 14

Challenge level

My measurements have got all jumbled up! Swap them around and see if you can find a combination where every measurement is valid.
problem
A long time at the till

Age

14 to 18

Challenge level

Try to solve this very difficult problem and then study our two suggested solutions. How would you use your knowledge to try to solve variants on the original problem?
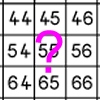
problem
What do you need?

Age

7 to 11

Challenge level

Four of these clues are needed to find the chosen number on this grid and four are true but do nothing to help in finding the number. Can you sort out the clues and find the number?
problem
Cows and sheep

Age

7 to 11

Challenge level

Use your logical reasoning to work out how many cows and how many sheep there are in each field.
problem
A bag of marbles

Age

5 to 7

Challenge level

Use the information to describe these marbles. What colours must be on marbles that sparkle when rolling but are dark inside?
problem
Road maker 2

Age

16 to 18

Challenge level

Can you work out where the blue-and-red brick roads end?
problem
Impossible triangles?

Age

16 to 18

Challenge level

Which of these triangular jigsaws are impossible to finish?