Polyhedra

problem
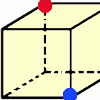Redblue

Age

7 to 11

Challenge level

Investigate the number of paths you can take from one vertex to another in these 3D shapes. Is it possible to take an odd number and an even number of paths to the same vertex?
problem
Which solid?

Age

7 to 16

Challenge level

This task develops spatial reasoning skills. By framing and asking questions a member of the team has to find out what mathematical object they have chosen.
problem
Icosian game

Age

11 to 14

Challenge level

This problem is about investigating whether it is possible to start at one vertex of a platonic solid and visit every other vertex once only returning to the vertex you started at.
problem
Triangles to tetrahedra

Age

11 to 14

Challenge level

Imagine you have an unlimited number of four types of triangle. How many different tetrahedra can you make?
problem
Which solids can we make?

Age

11 to 14

Challenge level

Interior angles can help us to work out which polygons will tessellate. Can we use similar ideas to predict which polygons combine to create semi-regular solids?
problem
Dodecawhat

Age

14 to 16

Challenge level

Follow instructions to fold sheets of A4 paper into pentagons and assemble them to form a dodecahedron. Calculate the error in the angle of the not perfectly regular pentagons you make.
problem
Proximity

Age

14 to 16

Challenge level

We are given a regular icosahedron having three red vertices. Show that it has a vertex that has at least two red neighbours.
problem
Three cubes

Age

14 to 16

Challenge level

Can you work out the dimensions of the three cubes?
problem
Tetrahedra tester

Age

14 to 16

Challenge level

An irregular tetrahedron is composed of four different triangles. Can such a tetrahedron be constructed where the side lengths are 4, 5, 6, 7, 8 and 9 units of length?
problem
Platonic planet

Age

14 to 16

Challenge level

Glarsynost lives on a planet whose shape is that of a perfect regular dodecahedron. Can you describe the shortest journey she can make to ensure that she will see every part of the planet?