Perimeter

game
Favourite

Dicey perimeter, dicey area

Age

7 to 11

Challenge level

In this game for two players, you throw two dice and find the product. How many shapes can you draw on the grid which have that area or perimeter?
problem
Shape draw

Age

7 to 11

Challenge level

Use the information on these cards to draw the shape that is being described.
problem
Numerically equal

Age

7 to 11

Challenge level

Can you draw a square in which the perimeter is numerically equal to the area?
problem
Shapes on the playground

Age

7 to 11

Challenge level

Sally and Ben were drawing shapes in chalk on the school playground. Can you work out what shapes each of them drew using the clues?
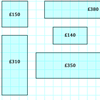
problem
Through the window

Age

7 to 11

Challenge level

My local DIY shop calculates the price of its windows according to the area of glass and the length of frame used. Can you work out how they arrived at these prices?
problem
Perimeter expressions

Age

11 to 14

Challenge level

Create some shapes by combining two or more rectangles. What can you say about the areas and perimeters of the shapes you can make?
problem
Changing areas, changing perimeters

Age

11 to 14

Challenge level

How can you change the area of a shape but keep its perimeter the same? How can you change the perimeter but keep the area the same?
problem
Can they be equal?

Age

11 to 14

Challenge level

Can you find rectangles where the value of the area is the same as the value of the perimeter?
problem
Perimeter possibilities

Age

11 to 14

Challenge level

I'm thinking of a rectangle with an area of 24. What could its perimeter be?
problem
Perimeter challenge

Age

11 to 14

Challenge level

Can you deduce the perimeters of the shapes from the information given?