Odd and even numbers

In how many different ways can you break up a stick of seven interlocking cubes? Now try with a stick of eight cubes and a stick of six cubes. What do you notice?

How will you complete these interactive Venn diagrams?

How would you create the largest possible two-digit even number from the digit I've given you and one of your choice?

Use the interactivities to fill in these Carroll diagrams. How do you know where to place the numbers?

What happens when you add three numbers together? Will your answer be odd or even? How do you know?

Four bags contain a large number of 1s, 3s, 5s and 7s. Can you pick ten numbers from the bags so that their total is 37?

This problem challenges you to find out how many odd numbers there are between pairs of numbers. Can you find a pair of numbers that has four odds between them?

This problem looks at how one example of your choice can show something about the general structure of multiplication.

Are these statements always true, sometimes true or never true?

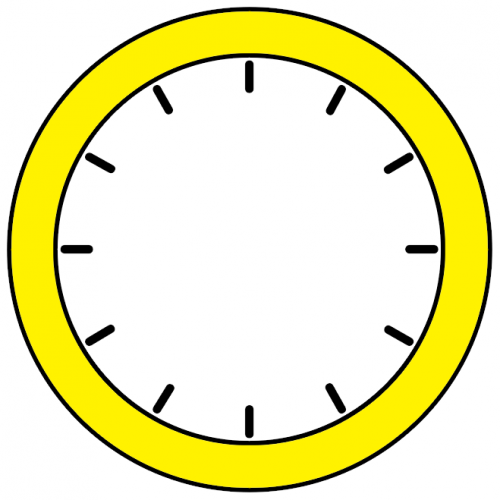
There is a clock-face where the numbers have become all mixed up. Can you find out where all the numbers have got to from these ten statements?