Fractions
-

-
 problem
problemFamily fortune
If three brothers will get £20 more if they do not share their money with their sister, how much money is there?
-
 problemFavourite
problemFavouriteFractions jigsaw
A jigsaw where pieces only go together if the fractions are equivalent.
-
 problemFavourite
problemFavouriteKeep it simple
Can all unit fractions be written as the sum of two unit fractions?
-
 problemFavourite
problemFavouriteDiminishing returns
How much of the square is coloured blue? How will the pattern continue?
-

-
 problemFavourite
problemFavouriteFractions rectangle
The large rectangle is divided into quadrilaterals and triangles. Can you untangle what fractional part is represented by each of the ten numbered shapes?
-
 problemFavourite
problemFavouriteSame answer
Aisha's division and subtraction calculations both gave the same answer! Can you find some more examples?
-
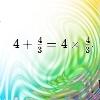 problem
problemSum equals product
The sum of the numbers 4 and 1 [1/3] is the same as the product of 4 and 1 [1/3]; that is to say 4 + 1 [1/3] = 4 × 1 [1/3]. What other numbers have the sum equal to the product and can this be so for any whole numbers?
-
 problem
problemPlutarch's boxes
According to Plutarch, the Greeks found all the rectangles with integer sides, whose areas are equal to their perimeters. Can you find them? What rectangular boxes, with integer sides, have their surface areas equal to their volumes?
