Factors and multiples
-
 problemDoes a graph of the triangular numbers cross a graph of the six times table? If so, where? Will a graph of the square numbers cross the times table too?
problemDoes a graph of the triangular numbers cross a graph of the six times table? If so, where? Will a graph of the square numbers cross the times table too? -
 problemFavourite
problemFavouriteWhich is quicker?
Which is quicker, counting up to 30 in ones or counting up to 300 in tens? Why?
-
 problemFavourite
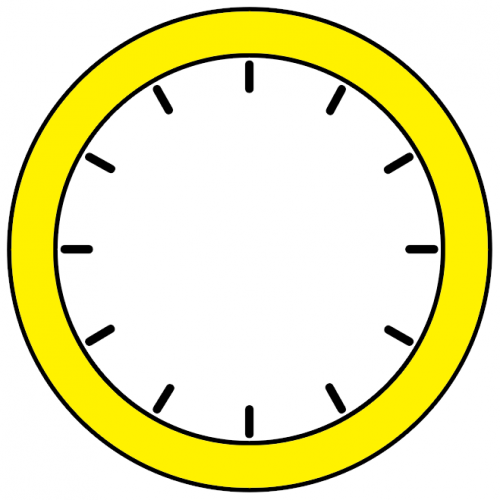
problemFavouriteA mixed-up clock
There is a clock-face where the numbers have become all mixed up. Can you find out where all the numbers have got to from these ten statements?
-
 problem
problemColour wheels
Imagine a wheel with different markings painted on it at regular intervals. Can you predict the colour of the 18th mark? The 100th mark?
-
 problem
problemNumber tracks
Ben's class were cutting up number tracks. First they cut them into twos and added up the numbers on each piece. What patterns could they see?
-
 problemFavourite
problemFavouriteMusic to my ears
Can you predict when you'll be clapping and when you'll be clicking if you start this rhythm? How about when a friend begins a new rhythm at the same time?
-
 problemFavourite
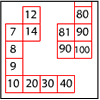
problemFavouriteMultiplication square jigsaw
Can you complete this jigsaw of the multiplication square?
-
 problemFavourite
problemFavouriteWhat's in the box?
This big box multiplies anything that goes inside it by the same number. If you know the numbers that come out, what multiplication might be going on in the box?
-
 problemFavourite
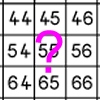
problemFavouriteWhat do you need?
Four of these clues are needed to find the chosen number on this grid and four are true but do nothing to help in finding the number. Can you sort out the clues and find the number?
-
 problem
problemThree spinners
These red, yellow and blue spinners were each spun 45 times in total. Can you work out which numbers are on each spinner?
