Each time you visit the NRICH site there will be some activities which are 'live'. This means we are inviting students to send us solutions, and we will publish a selection of them, along with each student's name and their school, a few weeks later. If you'd like to know more about what we're looking for, read this short article.
The last day for submitting solutions to these live problems is Monday 9 June.
Live problems
No live problems at the moment
Recently solved problems
-
problemFavouriteWhich is bigger?
Age14 to 16Challenge level
Which is bigger, n+10 or 2n+3? Can you find a good method of answering similar questions?
-
problemFavouriteSealed solution
Age7 to 14Challenge level
Ten cards are put into five envelopes so that there are two cards in each envelope. The sum of the numbers inside it is written on each envelope. What numbers could be inside the envelopes?
-
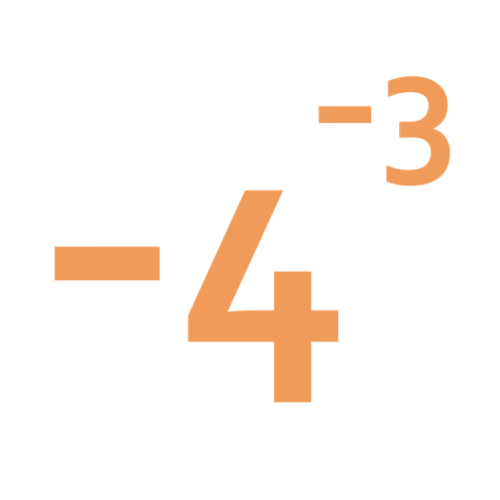problemFavouriteClimbing complexity
Age11 to 14Challenge level
In the 2020 Olympic Games, sport climbing was introduced for the first time, and something very interesting happened with the scoring system. Can you find out what was interesting about it?
-
problemFavouriteCharlie's delightful machine
Age11 to 16Challenge level
Here is a machine with four coloured lights. Can you develop a strategy to work out the rules controlling each light?
-
problemFavouriteShifting times tables
Age11 to 14Challenge level
Can you find a way to identify times tables after they have been shifted up or down?
-
problemFavouriteKeep it simple
Age11 to 14Challenge level
Can all unit fractions be written as the sum of two unit fractions?
-
problemFavouriteFinding factors
Age14 to 16Challenge level
Can you find the hidden factors which multiply together to produce each quadratic expression?