Venn diagram fun
Can you create a Venn diagram?
Problem
A Venn diagram is a way of representing all possible logical relationships between a collection of sets.
The image shows a Venn diagram for three sets $A$, $B$ and $C$
Image
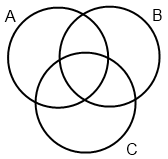
How would you describe each of the seven regions in the diagram using unions $\cup$ and intersections $\cap$ of $A, B, C, A^c, B^c, C^c$ where the complements $A^c, B^c$ and $C^c$ of the sets $A, B$ and $C$ are the sets of elements not contained in $A, B$ and $C$ respectively relative to a universal set $A\cup B\cup C$
Create a Venn diagram for 4 sets $A$, $B$, $C$ and $D$. Make sure that your diagram contains regions for all possible intersections and you might like to experiment to create a particularly pleasing diagram.
Did you know ... ?
Venn diagrams are useful in many problems in logic, probability, computer science and set theory. As well as a useful tool, they are an area of study in themselves and much research has gone into the creation of particularly beautiful or symmetric Venn diagrams for larger numbers of sets.
Venn diagrams are useful in many problems in logic, probability, computer science and set theory. As well as a useful tool, they are an area of study in themselves and much research has gone into the creation of particularly beautiful or symmetric Venn diagrams for larger numbers of sets.
Student Solutions
Consider the Venn diagram for 3 sets $A$, $B$ and $C$ with each of the $7$ regions labelled as follows
Image
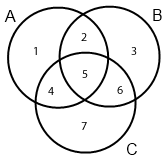
The set-theoretic representation of these regions is
1. $C^c\cap B^c$
2. $A\cap B \cap C^c$
3. $A^c \cap C^c$
4. $A\cap C \cap B^c$
5. $A\cap B\cap C$
6. $B\cap C \cap A^c$
7. $A^c \cap B^c$
A four-region diagram can be constructed by overlapping four rectangles (blue, pink, yellow, red) as follows:
Image

Note that there are $15$ distinct regions of the diagram, corresponding to $2^4-1$. Make sure your diagram has exactly 15 regions!
