Some Spirals and Tessellations

Image

Aspiral is a curve formed by a point moving around a fixed point and constantly moving away from or approaching the fixed point.

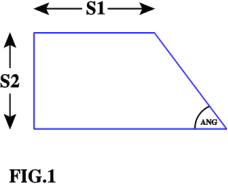
This month, building on the idea that many sets of things can be placed in a spiral configuration, we consider the following program based on Fig.1:

TO TRAP :S1 :S2 :ANG
IF :S1 > 100 [STOP]
FD :S1 RT :ANG
FD :S2/SIN :ANG RT (180 - :ANG)
FD :S1 + :S2 * TAN (90 - :ANG) RT 90
FD :S2 RT 90 FD :S1 LT (90 - :ANG)
TRAP :S1/SIN :ANG :S2/SIN :ANG :ANG
END

Image

Image

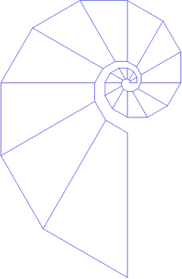
Try TRAP 5 25 60 as a starter for your investigations. See what spirals you can generate now.

While still in the realm of geometry a consideration of tessellations, tiles and tilings is long overdue.

Cundy C.M. and Rollett A. P. in 'Mathematical Models' give a good introduction to the plane tessallations.

First consider the three regular tessellations based on the square, equilateral triangle and regular hexagon respectively as below.

Image

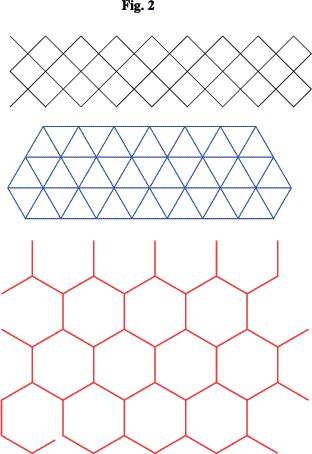
Can you devise a set of elegant procedures to illustrate these somewhat lacklustre tilings? But colour them much more imaginatively! [Hint: try drawing them freehand before thinking about construction procedures.]