Real(ly) numbers
Problem
If $x$, $y$ and $z$ are real numbers such that:
$x+y+z=5$
and $xy+yz+zx=3$,
what is the largest value that any one of these numbers can have?
Getting Started
Student Solutions
Alan of Madras College, St Andrew's and Tom of Bosworth College, Desford, Leicestershire, sent in really elegant solutions to show the maximum value taken by any one of these variables.
Firstly Alan's solution
Consider the function,
$$f(a) = (a - x)(a - y)(a - z)$$
which has the real solutions, $a = x$, $a = y$ and $a = z$. when $f(a) = 0$.
$$\eqalign{ f(a) &=& a^3 - (x + y + z)a^2 + (xy + yz + zx)a - xyz \\ \; &=& a^3 - 5a^2 + 3a - xyz}$$
Differentiating with respect to $a$ (where $x$, $y$ and $z$ are constant in respect to $a$),
$$\eqalign{ f`(a) &=& 3a^2 - 10a + 3 \\ \; &=& (3a - 1)(a - 3)}$$
This gives the coordinates of the turning points of the graph as $a = 3$ and $a = 1/3$. As $x$, $y$ and $z$ are real, the solutions of $f(a) = 0$ must also be real, which gives:
$$x \leq 1/3 \leq y \leq 3 \leq z$$
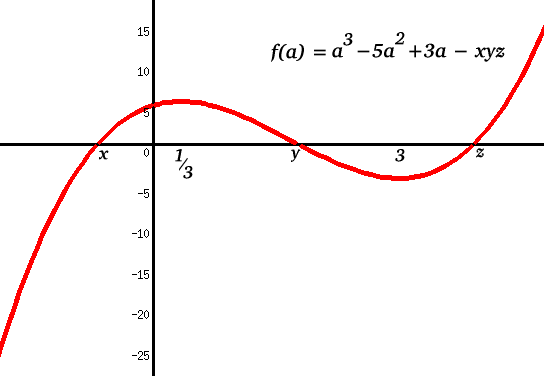
Considering the graph, which cuts the horizontal axis in a = x , a = y and a = z , in order to make z as large as possible the graph is dropped down as far as possible making x = y = 1/3 and z = 13/3.
Thus 13/3 is the maximum real value of one of the solutions of f ( a ) = 0 which corresponds exactly to the given equations, that is 13/3 is the maximum real value for any of the variables where all three satisfy the given equations.
The same method gives the minimum value . By lifting the graph the minimum possible value of x is made to occur when y = z = 3 which gives x = -1. So x = -1 is the minimum real value possible for any of the variables satisfying the given equations.
Tom uses a different method. He treats the two equations as simultaneous equations and one of the variables as if we know its value. Since the variables are interchangeable, this can be any of them. We can choose one of the variables to be bigger than the others and the limits we obtain on this variable can be applied to all of them.
Here is Tom's solution to the problem
We have $x+y+z=5$ so taking $y=5-x-z$:
$$\eqalign{ xy + yz + zx &= 3 \\ x(5-x-z) +z (5-x-z) +zx &= 3 \\ z^2 - z(5 - x) - (5x - x^2 - 3) = 0 }$$
As z is a real number we use the condition for this quadratic equation to have real solutions:
$$25 - 10 x + x^2 + 20 x - 4 x^2 - 12 = 13 + 10x -3x^2 \geq 0 .$$
This tells us the range of possible values for $x$. Looking at the graph of the function: $f ( x ) = 13 +10 x - 3 x^ 2$, we see it cuts the axes at (0, 13) (-1, 0) and (13/3, 0) and has its maximum value when $x = \frac{10}6 = \frac53$.
|
|
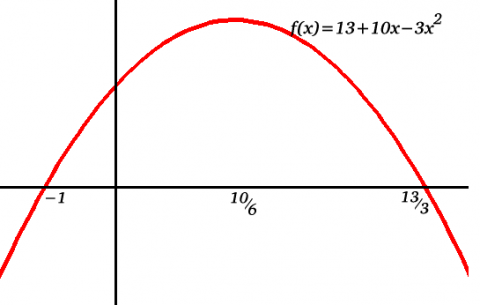
So 13/3 is the maximum value any of the numbers can take and -1 is the minimum value any of the variables can take.
Here's another solution from Ana: solution .
