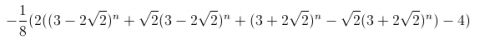We had some good international thinking on this stimulating investigation from a wide range of ages, with some experimental computation and analytical reasoning. I was delighted by the levels of creativity displayed. There are clearly some great mathematicians in the making!
Joe from Flegg High School, Kiran from John Lyon School both found the 'first' answer 20, 21 and 29 and Filipe also found 119, 120, 169 and 696, 697, 985
Gilbert, Mookie and Kyle from Li Po Chun United World College of Hong Kong said:
We designed an Excel programme in order to find the examples that the smaller triples differ by one so that we could, hopefully, find the pattern of them and find out a general solution of them. Considering the 65534 numbers, which is the maximum number of rows that Excel provides, we have found that there are 7 sets of solutions.
Freddie from Kingston Grammar School
Using Excel, I have found that there are six such triples with the smallest number below 100,000. I did this by calculating $\sqrt{n^2 + (n+1)^2}$ and looking for integers (using integer n's).
The triples are:
3,4,5;
20,21,29;
119,120,169;
696,697,985;
4059,4060,5741;
23660,23661,33461
Mahdokht from Farzanegan of Kermanshah used the formula which generates all Pythagorean triples which don't share a common factor: If $a^2+b^2=c^2$ then there are natural numbers $m> n\geq 1$ for which $$a=mn, b=\frac{m^2-n^2}{2}, c=\frac{m^2+n^2}{2}$$ Mahdokht then investigated solving $b=a+1$ and found the equation
$$m^2-2mn -n^2-2=0$$ The solution is $$m = n \pm \sqrt{2n^2+2}$$ and, as Mahdokht points out, this mean that $2n^2+2$ must be a square number. Using this as a guide, Mahdokht found the triples 20, 21, 29 and 119, 120, 169.
Eleanor from Dr. Challoner's High School made a wonderful observation in her solution:
Using a spreadsheet I calculated the next 4 Pythagorean triples where the smaller 2 numbers differ by 1. These were, as well as 3, 4, 5 : 20, 21, 29 119, 120, 169 696, 697, 985 4059, 4060, 5741 I began investigating the differences between each of the third numbers. A pattern seemed to appear: 29/5 = 5.8 169/29 = 5.827586..... 985/169 = 5.828402..... 5741/985 = 5.828426..... The amount that the third number in each triple is multiplied by to get the next third number in the triple seems to be tending towards $3+2\sqrt{2}$ (5.8284271....)
To test this I multiplied 5741 by $3+2\sqrt{2}$, which gave me 33461.00012...
Using the closest integer 33461, I found using my spreadsheet that this is indeed a Pythagorean triple in which the smaller numbers differ by 1: $23660^2 + 23661^2 = 33461^2$
Repeating this once again, multiplying 33461 by $3+2\sqrt{2}$, I get 195025. This too is the third number in a triple: $137903^2 + 137904^2 = 195025^2$
Thus it seems that the third number in each triple (where the smallest numbers differ by 1) is $3+2\sqrt{2}$ times the third number of the previous triple.
Sam from Bridgewater High School said
After considering this problem for a while it proved rather challenging. I started off by constructing a Diophantine equation (an equation that the solutions have to be integers) and with the help of the computer found a formula for one of the 3 values in the Pythagorean triple:
I feel, if my fomula is correct, which is has been for a far a I have tested it which is up to about n=100 but after that the values are too large for the computer to hand. To work out each triplet just put a value n into the fomula that is 2 or bigger and an integer and it will give the 2nd longest side. Here are my first few examples:
3 4 5
20 21 29
119 120 169
696, 697 985
4059 4060 5741 ,
23660 23661 33461
137903 137904 195025
803760 803761 1136689
4684659 4684660 6625109
27304196 27304197 38613965
159140519 159140520 225058681
927538920 927538921 1311738121
5406093003 5406093004 7645370045
31509019100 31509019101 44560482149
William from Barnton Community Primary School explored in a similar way, and said (in an exceptionally creative solution)
$$ \begin{matrix} 0^2 + 1^2 &=& 1^2\\ 3^2 + 4^2 &=& 5^2\\ 20^2 + 21^2 &=& 29^2\\ 119^2 + 120^2 &=& 169^2\\ 696^2 + 697^2 &=& 985^2\\ 4,059^2 + 4,060^2 &=& 5,741^2\\ 23,660^2 + 23,661^2 &=& 33,461^2\\ \end{matrix} $$
I used Excel to scan through all of the square numbers up to $h^2+(h+1)^2=60000$. I then found the ratio between each finding. It tended towards $3+2\sqrt{2}$. From there I found how to get from one number to the next.
If $a_n^2 + (a_n+1)^2 = b_n^2$ and $a_1 = 0$ and $b_1 = 1$ then:
$R=3+2\sqrt{2}$
$a_n=\mbox{int}(a_{n-1}R)+3\quad \mbox{int}(b_{n-1}R)$
That gives me: $$ \begin{matrix} 23,660^2 + 23,661^2 = 33,461^2\\ 137,903^2 + 137,904^2 = 195,025^2\\ 803,760^2 + 803,761^2 = 1,136,689^2\\ 4,684,659^2 + 4,684,660^2 = 6,625,109^2\\ 27,304,196^2 + 27,304,197^2 = 38,613,965^2\\ 159,140,519^2 + 159,140,520^2 = 225,058,681^2\\ 927,538,920^2 + 927,538,921^2 = 1,311,738,121^2\\ 5,406,093,003^2 + 5,406,093,004^2 = 7,645,370,045^2\dots \end{matrix} $$
We invite you to consider if this method will always work and to consider why it works.
Matthew from QE Boys school presented us with a marvellous solution. I was so pleased to see such levels of mathematical creativity and this is well worth trying to understand. Well done to you Matthew!
By beginning with the obvious statement $n^2+(n+1)^2=(n+a)^2$, with $n$ and $a$ both in the natural numbers, it is possible to immediately reduce the statement to an equation for $n$ in $a$. $$n^2+(n+1)^2=(n+a)^2 \Leftrightarrow n=a-1\pm \sqrt{2a(a-1)}$$
It is immediately obvious that any $a$ which is a natural number > 1 and for which $\sqrt{2a(a-1)}$ is also a natural number generates a value $n$ which has the desired property. By rewriting the square root as $2a(a-1)=b^2$, where $b$ is an integer, a second quadratic equation can be realised: $$2a^2-2a-b^2=0 \Leftrightarrow a=\frac{1 \pm \sqrt{2b^2+1}}{2}$$ By letting $(b+c)^2=2b^2+1$, with $c$ in the integers, as above, a third quadratic equation can be formed: $$(b+c)^2=2b^2+1 \Leftrightarrow b=c \pm \sqrt{2c^2-1}$$ Repeating this process again, defining $(c+d)^2=2c^2-1$ results in the quadratic equation: $$c=d \pm \sqrt{2d^2+1}$$ Repeating this any more times causes the sign of the $1$ in the square root to alternate, but otherwise results in the same equation, with different (and quickly running out) variable names. This can be interpreted as a sort of recurrence relation. It is also not a terrible idea to make clear that there is presently no guarantee that an integer term in this relation will generate another integer term. Due to the context of the values (ie. their intended use), the negative values should be disregarded completely, as they simply generate duplicate triples. Similarly, the $(0,1,1)$ triple has been disregarded, as it is a trivial triple, and hence of no real significance. Hence, let $z_{x+1}=z_x+\sqrt{2z_x^2+(-1)^x}$ and $z_1=2$, $2$ being the value which generates the $(3,4,5)$ triple. It is clearly now the case that $z_{2x+1}$ will generate a Pythagorean triple (and, more specifically, a primitive triple with a difference of 1 between the smaller legs), provided that $z_{2x+1}$ and $\sqrt{2z_{2x+1}^2+1}$ are both integers, which, due to the definition of $z_x$ , indicates that it is necessary and sufficient that $z_{2x+1}$ and $z_{2x+2}$ are integers.
After a small amount of algebraic manipulation, it may be seen that
$$2z_{x+1}^2+(-1)^x=(2z_x+\sqrt{2z_x^2+(-1)^{x+1}})^2,$$ and this can be used as the basis for mathematical induction on $\sqrt{2z_{x+1}^2+(-1)^x}$. Use $z_1=2, 2z_1^2+1=9$ as the base case for the aforementioned induction, and observe that $\sqrt{2z_{x+1}^2+(-1)^x}=2z_x+\sqrt{2z_x^2+(-1)^{x+1}}$.
Hence, if $\sqrt{2z_x+(-1)^{x+1}}$ is an integer, then $z_x$ is also an integer and so is $\sqrt{2z_{x+1}^2+(-1)^n}$. Because the base case is true, and every preceding case's truth confirms its successor's truth, it is instantly seen that every term in the sequence is an integer (and, hence, every odd term in the sequence is a candidate value for $b$ and can be used to generate a triple). Finally, by simplifying the quadratic equations out from the beginning of the process, it can be seen that $n_x=z_{2x-1}+\frac{\sqrt{2z_{2x-1}^2+1}-1}{2}$, and hence that $n_x^2+(n_x+1)^2=(z_{2x-1}+\sqrt{2z_{2x-1}^2+1})^2$.
As it has already been proven that $\sqrt{2z_{2x-1}^2+1}$ is an integer for all $x$, this is an additional confirmation that the solutions generated are valid. This also describes the relationship between the longest leg of the triple and the even-indexed $z$ values: $$n_x^2+(n_x+1)^2=z_{2x}$$ From this, it is possible to create each triple from the previous, starting from the smallest and working up infinitely. This, as well as other results, prove that there are infinitely many triples where the shorter legs differ by 1. However, as the sequence was not shown as the only one that generates such triples, it is possible that not all triples with this property will be generated.
I ran this on a spreadsheet to check and this does indeed generate the required sides - you might like to explore this idea further