Pegboard Quads

This solution was submitted by Michael of St John Payne school. Does anyone have any other ideas?

Image

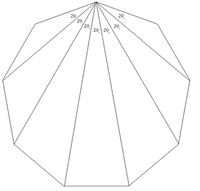
Image

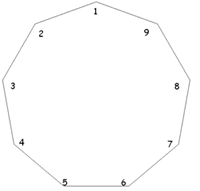
If we draw lines from a particular vertex to every other, then the angle separating $2$ adjacent vertices is $20^\circ$ (Can you explain this? -- Ed.) . If we label the polygon as shown in the right hand diagram, the angle $416$ is going to be two lots of $20^\circ$ and therefore $40^\circ$. This means that we have a general rule:

Angle $ABC = 20 \times (|A-C|)$ when A > C and A > B or A < C and A < B . But this will only work for angles where $B$ isn't between $A$ and $C$. For angles where $B$ is between $A$ and $C$ we need to go the long way round the polygon from $A$ to $C$, or in other words the whole polygon take away $A$ to $C$. So we can come up with the rule: Angle $ABC = 20 \times ( 9 - |A-C| )$ for any angle where A < B < C or A > B > C .

E.g. Angle $124 = 20 \times (9 |1-4| ) = 20 \times 6 = 120$

We can use these rules to show that the angles in any quadrilateral $ABCD$ on the pegboard must add up to $360^\circ$. If you rotate the peg board so that $A$ is always at point $1$ then $ABC$ and $BCD$ will obey the second rule and $CDA$ and $DAB$ will obey the first rule. Therefore \begin{eqnarray} ABC + BCD + CDA + BAC &=& 20 \times (9-|A-C|)+20 \times (9-|B-D|)+20 \times (|C-A|)+20 \times (|D-B|)\\ &=&360. \end{eqnarray} We can also deduce that $2$ opposite of the quadrilateral angles will add up to $180^\circ$: For quadrilateral $ABCD$, where the pegboard is rotated so that point $A$ is on peg $1$, Angle $ABC$ will obey the first rule and Angle $CDA$ will obey the second rule. Therefore

\begin{eqnarray} 20 \times ( 9 - |A-C|) + 20 \times (|A-C|) &=& \mbox{ sum of to opposite angles} \\ & = &20 \times (9 - |A-C| + |A-C| ) \\ &=& 20 \times 9 = 180^\circ \end{eqnarray}