Keep on halving

Image

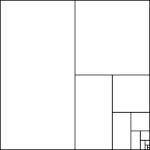
Imagine a square of paper divided in half, and then one of those halves divided again, and so on. It might look like this...

In the pictures below, some of the rectangles are shaded according to a pattern.

Can you work out the shaded amounts if the process continued forever?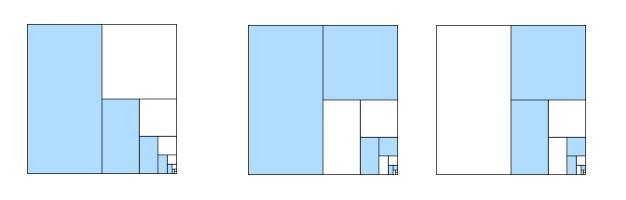

Image

One way of representing the shaded amount is to use a binary representation. The first digit after the point represents the halves, the second digit represents the quarters, and so on.

 

Image

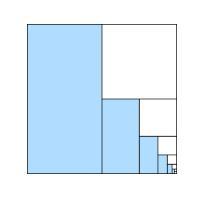
So the image on the right would be represented by $0.10101010\ldots$ which can be written $0.\dot{1}\dot{0}$.

You can think of this as a $1$ in the $2^{-1}$ column, a $0$ in the $2^{-2}$ column, a $1$ in the $2^{-3}$ column and so on.

 

One method for working out the representation of a fraction is as follows:

1) Double the fraction.

2) If the answer is greater than 1, write a 1 after the point. Discard the whole number part.

3) If the answer is less than 1, write a 0 after the point.

4) Double the new fraction, and repeat.

 

Try this iterative process out for the fractions represented in the pictures above.

 

Here are some questions to consider:

 

Can you explain how the iterative process works?

Can every rational number between 0 and 1 be represented in this way? How do you know?

What is special about $0.01010101\ldots$, $0.001001001001\ldots$, $0.000100010001\ldots$ and so on?

What is the relationship between $0.01010101\ldots$ and $0.101010101\ldots$? Why?