It's times again
Problem
It's Times Again printable sheet
On the table in front of you is a grid like this:

Each of the letters stands for a different number. The numbers go up in size from the top left to the bottom right, so 'a' is smaller than 'b', 'b' is smaller than 'c', etc. But the numbers might not be consecutive and they might not be going up by the same amount each time, so the first line could be something like this:

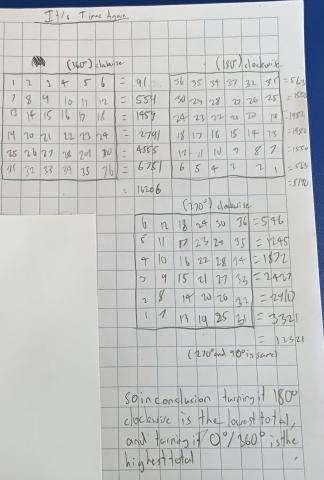
Imagine that you have another version of this grid (with the same numbers), but this one is made of plastic that you can see through. You place the plastic one over the other grid so that it covers it completely. You can flip it over and/or turn it around as you put it down. Now, each pair of numbers (one above the other) is multiplied together, and all of these products
are added together.
Your challenge is to say which way of flipping over and/or turning the plastic grid will give you the highest total and which way will give you the lowest total.
Getting Started
One way to start would be to consider a smaller grid filled with numbers. Perhaps the numbers are all very close together, or perhaps some are much larger than others.
You can use tracing paper to make another version of your grid, and consider some different ways of placing it on top. Without doing all of the calculations, can you see which products are going to be the largest?
Student Solutions
If anybody else has a solution they would like to share with us, please email us your ideas.
Teachers' Resources
Why do this problem?
Possible approach
The six by six grid can be printed out for pupils to use, either with the letters or as a blank grid, and pupils might want to use tracing paper in order to create a see-through version of the grid. The challenge will need to be explained very clearly so as to prevent a lot of unnecessary calculations being made.
Key questions
Why do you think that this will give the highest/lowest total?
What would happen if the numbers in the grid are all very close together, like consecutive numbers?
What about if the final number in the grid is much bigger than all of the other numbers? What if the final row of numbers are all very large?
Possible support
Pupils could explore a smaller grid, such as this three by three grid, and some pupils will find this task more accessible if they are given a grid filled with numbers rather than letters, such as in the task So It's Times.
Possible extension
Pupils might like to consider variations on this activity - what if the letters on a grid don't necessarily stand for different numbers, so the numbers can either stay the same or increase as you move through the grid? What if the letters all represent fractions or decimals between 0 and 1?