So it's times!
Problem
So It's Times! printable sheet
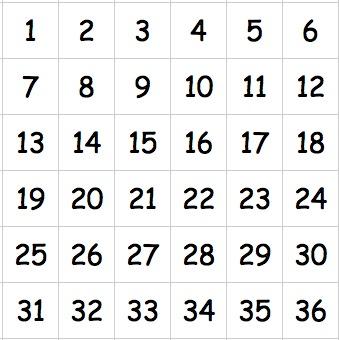
On the table in front of you is a grid like this:
Imagine that you have another version of this grid (with the same numbers), but this one is made of plastic that you can see through. You place the plastic one over the other grid so that it covers it completely. You can flip it over and/or turn it around as you put it down. Now, each pair of numbers (one above the other) is multiplied together, and all of these products are added together.
Your challenge is to say which way of flipping over and/or turning the plastic grid will give you the highest total and which way will give you the lowest total, without calculating and adding together the 36 multiplications.
Getting Started
One way to start would be to print off the grid and use tracing paper to make another version of it. Have a think about the different ways that you could place it on top - how many ways of doing this are there? Choose one way and then (without doing all of the calculations) consider which products are going to be the largest. Is there a different way you could turn it to make more or fewer large products?
If you are stuck, you can start with a small grid (perhaps two by two or three by three). Choose a way of putting the second grid on top, and then calculate and add together all of the multiplications. What do you notice?
Student Solutions
Zach sent in a wonderful solution which you can read about at length here: So Its Times - Zach T.pdf
It starts off as follows:
Saksham from Hounslow Town Primary School wrote:
So first I wrote out all the possible multiplication facts: 1 x 1, 1 x 6, 1 x 31, 1 x 36
Then I decide which one was the biggest and then I did that to all of the facts. After I tallied them and found out which one had the most tallies therefore would give the largest answer.
I have attached a replica of what I did but in excel as I couldn't attach the original file here: So its Times .xlsx
Allison from the The Glasgow Academy in Scotland wrote;
ANSWER : The highest total of flipping over would be to just place the second sheet over the top of the first one in exactly the same place. The lowest total of flipping over would be to place the sheet of plastic down over the first one 180 degrees turned around so that the number 1 is on top of the number 36 (for example).
WORKING : If you think about it, the highest numbers that you can reach are the ones that are multiplied by themselves. Your highest number is 36. So the highest number that you can get is 36 x 36= 1,296. As soon as you flip the second sheet around, the highest number gets much smaller. The largest number you can get now is 36 x 31=1,116. Therefore, the largest numbers are the ones that are multiplied by themselves. The moment you take that away, most of the numbers get much smaller.
Then, what would the smallest number be? Well we know that it can't be just placing the second sheet on top of the first one in the same way because that is how we get the largest number. So we could try multiplying 36 by the smallest number on the sheet which is 1. To do this we would need to turn the second sheet around so that 1 is on top of 36. Then the number 2 would be on top of 35 and so on. This means that it will have the smallest multiplications within the square so that the overall number will be the smallest number possible.
Ayobami from Woolwich Polytechnic School wrote:
Because we were told not to do the number calculations, we considered how we might use algebra to help. Firstly, Ayobami decided to use the nth term to solve the question and find a solution. He started seeing patterns in the nth term calculations, and realised that some of the answers were the same, before deciding a different approach. All the children started
using algebra on the grid by replacing the four corners with a,b,c and d, here is the total file:
Woolwich 2.doc or woolwich.pdf
Meghna from the The British School Kathmandu in Nepal said:
The way to get the highest total is by pairing each number with itself, i.e. 1 with 1, 2 with 2 and so on. This will give us the highest possible total as squaring a number will give a larger product than when we multiply the number by a number smaller than itself. For example, 5 x 5 = 25 whereas 5 x 4 = 20.
The way to get the lowest total is by pairing the largest number with the smallest, 36 with 1, 35 with 2 and so on. This will give us the lowest total, because as I mentioned above, pairing numerals with a number smaller than itself will give us a lower total. So to get the highest total, square each number and to get the lowest total, pair the biggest number with
the smallest, second biggest with the second smallest etc.
Thank you for all these wonderful solutions. It proved it be an activity that really made use of your multiplication facts.
Teachers' Resources
So It's Times!
This activity has been particularly created for the most able. (The pupils that you come across in many classrooms just once every few years.)
On the table in front of you is a grid like this:-
Why do this problem?
This problem is designed to challenge pupils both in number and spatial skills. It provides an opportunity for pupils to consider the properties of multiplication and to test their ideas.
Possible approach
If necessary before approaching the six by six array, present two sheets with a four by four array. Try not to go through it completely, but just try a couple of multiplications and then turn the top sheet over (or around, or both) and see what a few of the multiplications would be then.
The six by six grid can be printed out for pupils to use, and pupils might want to use tracing paper in order to create a see-through version of the grid. The challenge will need to be explained very clearly so as to prevent a lot of unnecessary calculations being made.
Key questions
What else could you explore?
Possible support
Pupils could explore a smaller grid, such as a three by three grid or a two by two grid. The restriction about not being allowed to calculate and add every multiplication can be relaxed on a smaller grid, and pupils can calculate which arrangement would give the highest and the lowest total. Pupils should then be encouraged to explain why they think this has happened, and whether or not they think the solution would be similar with a larger grid size.
Possible extension
Children could have a go at It's Times Again, which encourages children to explore how the problem changes if the numbers are no longer necessarily consecutive.