Extending Fraction Bars
This activity follows on from More Fraction Bars.
Look at these different coloured bars:
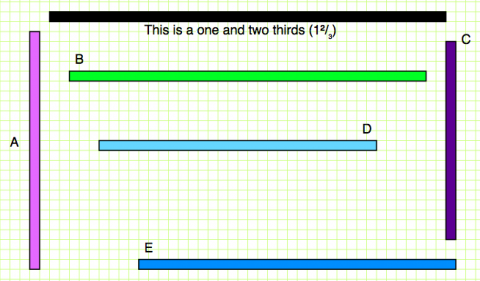
You might like to download a printable version of them here .
Put the bars in size order - can you do it without cutting them out?
Now focus on this bar:
This bar represents one whole and two thirds, or the number 1$\frac{2}{3}$. You might find it easier to think of it as a bar which is 'one whole' that has been stuck to a bar two-thirds the size of it.
We are thinking about all the other coloured bars as fractions of this bar, so we are thinking about them as fractions of 1$\frac{2}{3}$.
For example, look at Bar A below:
Drawing lines helps us measure it against the black bar:
What fraction of the black bar is Bar A?
Go through each of the other coloured bars and compare them to the black bar. What fraction of 1$\frac{2}{3}$ is each bar?
Write down your ideas for each bar. For example, you could write:
Bar A is three fifths of the black bar.
or
Bar A represents $\frac{3}{5}$ of 1$\frac{2}{3}$.
or
Bar A represents a whole.
Can you work out how we came up with these three ideas?
Can you find different ideas for what fraction of 1$\frac{2}{3}$ each bar represents?
Thank you to everybody who sent in their thoughts about this task.
Jacob from Stirling East Primary School in Australia explained how they started the activity:
I did it by counting the squares on the graph so that I could figure out how long the bars are so I could put them in size order.
Good idea, Jacob - it's really helpful to work out how long each bar is to begin with. James from Radstock Primary School in England used the lengths of the bars to work out what fraction each one represented:
Firstly, you need to count the number of squares in the black line (40). The black line is worth 1 and $\frac{2}{3}$ which is equal to $\frac{5}{3}$. Then, you can divide 40 by 5 which will get you 8. This is $\frac{1}{3}$ because you are dividing $\frac{5}{3}$ by 5.
$\frac{1}{3}$=8 If you halve this you will get $\frac{1}{6}$=4. Next, you have to count the number of squares in A(24), B(36), C(20), D(28) and E(32). You can now divide the number of squares in each bar by 4 which will tell you how many sixths there are in each bar. You can simplify these to make it easier to read.
A = $\frac{6}{6}$ = 1
B = $\frac{9}{6}$ = 1 and $\frac{3}{6}$ = 1 and $\frac{1}{2}$
C = $\frac{5}{6}$
D = $\frac{7}{6}$ = 1 and $\frac{1}{6}$
E = $\frac{8}{6}$ = 1 and $\frac{2}{6}$ = 1 and $\frac{1}{3}$
Now you can put them in ascending order (lowest to highest). C,A,D,E,B
We also had similar solutions sent in by Connie and Harry from Radstock Primary School - well done to all of you for explaining your ideas so clearly.
Reuben from New Cangle Primary School in the UK sent in the explanation below. Reuben has written each bar as a fraction of one whole, but also as a fraction of the black bar:
Thank you for sending in these ideas, Reuben. It's really interesting to see how we can represent numbers as a fraction of other numbers (in this case, as a fraction of 1$\frac{2}{3}$) even when those numbers are fractions themselves!
Extending Fraction Bars
This activity follows on from More Fraction Bars.
Look at these different coloured bars:
You might like to download a printable version of them here.
Put the bars in size order - can you do it without cutting them out?
Now focus on this bar:
This bar represents one whole and two thirds, or the number 1$\frac{2}{3}$. You might find it easier to think of it as a bar which is 'one whole' that has been stuck to a bar two-thirds the size of it.
We are thinking about all the other coloured bars as fractions of this bar, so we are thinking about them as fractions of 1$\frac{2}{3}$.
For example, look at Bar A below:
Drawing lines helps us measure it against the black bar:
What fraction of the black bar is Bar A?
Go through each of the other coloured bars and compare them to the black bar. What fraction of 1$\frac{2}{3}$ is each bar?
Write down your ideas for each bar. For example, you could write:
Bar A is three fifths of the black bar.
or
Bar A represents $\frac{3}{5}$ of 1$\frac{2}{3}$.
or
Bar A represents a whole.
Can you work out how we came up with these three ideas?
Can you find different ideas for what fraction of 1$\frac{2}{3}$ each bar represents?
Why do this problem
This activity gives pupils the opportunity to practise ordering and comparing fractions. It introduces the idea that as well as having a fraction of a whole number, you can also have a fraction of a fraction. Working together on this task will encourage pupils to build their fraction vocabulary.
Possible approach
Begin by showing some rods of different lengths on the IWB. Put a row of smaller rods together and show that this is the same length as a larger rod. Can pupils work out what fraction of the larger rod each smaller rod is? What if the larger rod represents 1$\frac{2}{3}$ - what fraction does the smaller rod represent now?In pairs or small groups, children should have access to multilink cubes, making each bar of the same colour throughout. Otherwise, pupils can use this sheet (word, pdf) along with some squared paper to make paper copies of each bar. It may be helpful for children to make multiple versions of the same bar in order to see that these can be fitted together to be the same length as the black bar.
Give pupils some time to investigate the order of size of the bars, and what fraction each bar represents. Bring the whole class together for a plenary - can the groups explain their choices? There may be disagreements between different groups and this can lead to a healthy discussion, encouraging each group to give reasons for their suggestion.
Key questions
Why is what you've chosen true?Can you think of a way of writing that down?
Tell me about your choice of fractions.
Possible extension
If a group or individual pupil has gone right to the end of the third part, ask them to look at each fraction and relate it to the other sizes, for example:"E is 1$\frac{1}{3}$ of A as E = 32 and A = 24."
See if children can work out what fraction is represented by each bar, as well as what fraction of the black bar they are.