Cut Nets
Each of the nets of nine solid shapes has been cut into two pieces. Can you see which pieces go together?
Age
7 to 11
Challenge level
The net of a cube has been cut into two. It could be put together in several ways so that it could be folded into a cube.
Image
Here are the nets of $9$ solid shapes. Each one of these has been cut into $2$ pieces, like the net of the cube.
Image
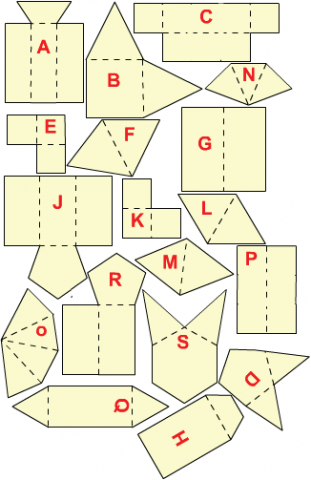
Can you see which pieces go together?
Printing out the shapes, cutting them out and folding them up may help. Here is a downloadable word document to help.
The shapes are a cube, cuboid, tetrahedron, square pyramid, pentagonal pyramid, hexagonal pyramid, triangular prism, pentagonal prism, trapezoid prism.
Hallie and Moira from Southbury Elementary in the US sent us the following:
When solving this problem, we found it easiest to look for similarities between the nets. One of the most obvious pairs were nets 'e' and 'k' because they are the same shape, each with 3 squares of the same size, so you could infer that when folded into their 3-D forms they will form a cube.
Another easier one was 'c' and 'p', because they have rectangles that have the same dimensions as each other. You could use this strategy (looking for equivalent dimensions) for other pairs too such as 'b' and 'f', 'l'and 'm', 'n' and 'd', and 'o' and 's'.
For sets like 'r' and 'j', 'h' and 'a' and 'g' and 'q', you find more similarity between the regular polygons such as the pair of trapezoids or hexagons. We also find it interesting that about
half of the nine figures are pyramid shapes and about half are prisms. We found it helpful to make a list and use process of elimination. We also cut out the shapes and folded and taped them to check our answers:
Image
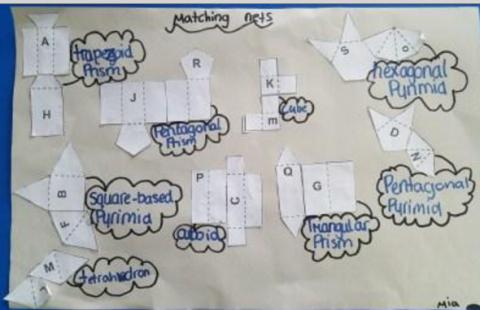
Brandon and Rebecca from Oakwood Academy send in the following picture:
Image
This is what their teacher wrote:
Two of our pupils at our SEN school have done really well with this challenge. They were given some support due to the nature of their learning needs.
Mia and IsabelleӬ, from Fordingbridge Junior School, wroteӬ
First we looked for similar 2D shapes and gently folded them to see if they created one of the finished 3D shapes. Then if it worked we would experiment to find out how the net would be put together. If it didn't work we would choose another piece of net with similar 2D shapes until we
found one that worked.
With the last few shapes we looked at how many sides the main shape, like a square, hexagon, pentagon or trapezium had and found another piece of net that could cover all of the sides. For example to find out that A and H worked we looked for two pieces with trapeziums on. Then we gently folded them together and it formed a 3D shape.
Image
We also had a number of solutions sent in from Cromer Junior School; namely Amy and Grace, Jacob, Owen and Ashley, Glen and Toby, Noah, Shannon, Aleesha and Brandon. Thank you for your good solutions.
Finally, Mr ArnoldӬ from The Gerrards Cross C of E SchoolӬ wrote:
Hi there. My class really loved working on Cut Nets. The attached file contains workings, reasoning and explanations on what they found, which they wrote themselves in small groups.
The Gerrards Cross C of E School.docx or The Gerrards Cross C of E School.pdf
Thank you everyone who sent in a solution. Keep up the good work and please send in further solutions to future live problems!
Cut Nets
The net of a cube has been cut into two. It could be put together in several ways so that it could be folded into a cube.
Image
Here are the nets of $9$ solid shapes. Each one of these has been cut into $2$ pieces, like the net of the cube.
Image
Can you see which pieces go together?
Why do this problem?
This problem makes children think hard about the nets of various polyhedra. It is not enough to know roughly what they look like. The number and shape of the faces and the way they are connected are important. It will help to develop children's visualisation skills and increase their familiarity with appropriate vocabulary. It provides an excellent opportunity for describing properties of 3D shapes.
Possible approach
You could start by talking about properties of some solid shapes with the group. One way to do this might be to hold up two shapes and ask them to talk about their similarities and differences. Depending on the children's experience you may need to explain what a net is, but they don't necessarily need to have worked extensively with nets in order to have a go at this problem.
You could introduce the problem on an interactive whiteboard or data projector but it would be helpful for children to have a copy of this sheet in pairs and to work together so that they are able to talk through their ideas with a partner. Scissors and sticky tape would be
useful!
Some children will relish the challenge of discovering for themselves which shapes have been used but some may work better knowing which they were to find. The shapes are: a cube, cuboid, tetrahedron, square pyramid, pentagonal pyramid, hexagonal pyramid, triangular prism, pentagonal prism, trapezoid prism.
Key questions
How do you think these two pieces could fit together?
Which piece could go with this one?
What shape are the faces on a ...?