Combinations of two
Can you make sense of this visual combinatorics proof?
Problem
Image
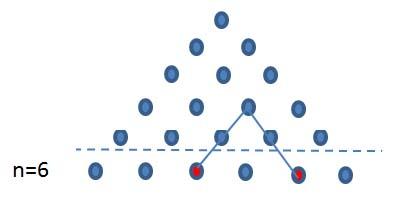
Can you use this diagram to prove that the number of different pairs of objects which can be chosen from six objects, $^6C_2$, is $$1 + 2 + 3 + 4 + 5?$$
Generalise this to show that the number of ways of choosing pairs from $n$ objects is
$$^nC_2 = 1 + 2 + ...+ (n-1) = \frac{1}{2}n (n - 1).$$
Did you know ... ?
The sum of the first $n$ whole numbers is called a triangle number because this sum can be represented geometrically by a triangular array of dots. The sum is easily found by working out the number of dots in the parallelogram formed by putting two triangular arrays side by side.
The sum of the first $n$ whole numbers is called a triangle number because this sum can be represented geometrically by a triangular array of dots. The sum is easily found by working out the number of dots in the parallelogram formed by putting two triangular arrays side by side.
Student Solutions
The diagram shows that every combination of two elements chosen from $6$ on the line $n = 6$ corresponds to exactly one dot in the triangular array above. This triangular array above the dotted line in the diagram represents the triangle number $T_5$. Conversely the diagram also shows that every dot in the triangular array for $T_5$ corresponds to one and only one of the choices of pairs of elements in the line $n=6$ . Hence the number of combinations of two elements chosen from $6$ is equal to $1 + 2 + 3 + 4 + 5$.
This generalises directly to finding the number of distinct pairs of elements chosen from $n$ elements. Draw the triangular array for $T_n$, that is rows of dots for $n = 1, 2, 3, ... n$. Now in the same way as for $n=6$, every pair of elements chosen from the bottom row can be joined by lines in the diagram to meet in a single dot in the array for $T_{n-1}$. Conversely each dot in $T_{n-1}$ corresponds to one and only one pair chosen from $n$ elements on the bottom line. This shows that the number of ways of choosing pairs from $n$ objects, generally denoted by $^nC_2$, is $$T_{n-1} = 1 + 2 + ...+ (n-1).$$ Putting two $T_{n-1}$ triangular arrays side by side gives $n(n-1)$ dots so $$^nC_2 = T_{n-1} = \frac{1}{2}n (n - 1).$$
