A calendar question
Problem
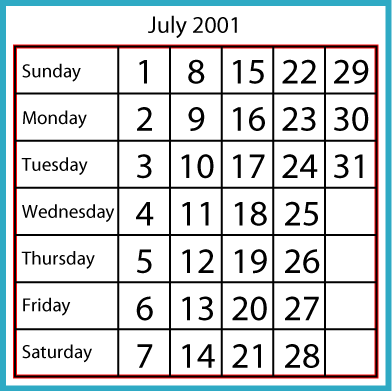
July $1$st $2001$ was on Sunday. July $1$st $2002$ was on Monday. July $1$st $2003$ was on Tuesday, but July $1$st $2004$ was on Thursday because $2004$ was a Leap Year.
When did July $1$st fall on a Monday again?
April $1$st $2002$ was on Monday. When did April $1$st fall on Monday again after that?
September $1$st $2003$ was on Monday. When did September $1$st fall on Monday again after that?
November $1$st $2004$ was on Monday. When did November $1$st fall on Monday again after that?
Getting Started
Do you know which years are leap years? They are the years which are divisible by $4$ so $2002$ was not a leap year but $2004$ was a leap year.
Why not make a table of results as you work them out?
Student Solutions
This was not only a first but also definitely a question for Mondays! So, when did July 1st fall on a Monday again, or April 1st, or September 1st or even November 1st?
Robert, Keiichi and Thomas , pupils at Moorfield Junior School, wrote that they solved the questions posed by trial and error. This is what they discovered for when July 1st falls over the next few years:
| Year | Day | Leap year or not? |
|---|---|---|
| 2004 - | Thur | [Leap year] |
| 2005 - | Fri | |
| 2006 - | Sat | |
| 2007 - | Sun | |
| 2008 - | Tues | [Leap year] |
| 2009- | Wed | |
| 2010- | Thurs | |
| 2011- | Fri | |
| 2012- | Sun | [Leap year] |
| 2013- | Mon |
So, is the answer that, in the year 2013, July 1st will again be on a Monday. Quite a wait! How old will you be then?
Anita, Louise, Jingjing are pupils from Kilvington Girls' Grammar School which is in Melbourne, in the state of Victoria in Australia, arrived at these answers for the other months:
Monday 1st Sept: 2008
Monday 1st Nov: 2010
Monday 1st April: 2013
Jade and Sarah , from Newland Primary School made a list to help them organise the information they needed to answer this problem. "This is how we worked it out", they write:
| 2001 | Monday |
| 2002 | Tuesday |
| 2003 | Wednesday |
| 2004 | Friday |
| 2005 | Saturday |
| 2006 | Sunday |
| 2007 | MONDAY! |
So, the answer is 2007. But for which month?
Not sure? If you see how solutions are arrived at, it really helps. Perhaps, this chart from Georgia (who lives in Suffolk in England) might help you decide.
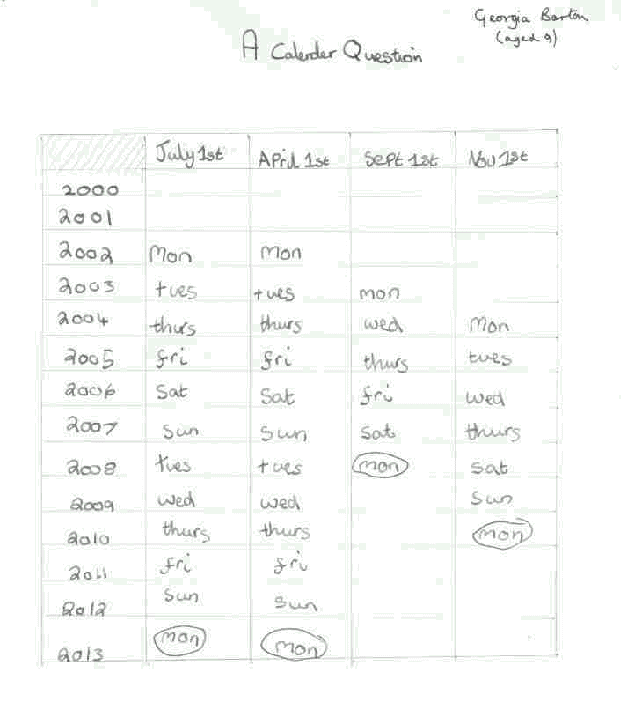
When you solve problems like this, try to see if there is a pattern in the answers. That will help you find the next answer you need. This is precisely what Kate did.
Kate provided a description of how finding a pattern helped her solve this problem and the thinking that was involved. Kate thinks she has clearly proven that her answer is correct. Read through and see if you agree with her.
If the date you are starting from is 3 years after a leap year, this will mean it is 5 years before the same date on the same day comes around again.
However, it the date is 2 years after a leap year, then it will mean 11 years before the same day on the same date comes around again.
1 year after a leap year will mean that it is 6 years before the same day comes again on the same date.
But, in a leap year there will be 6 years before the same day comes again on the same date.
A pattern occurs starting with July 1st 2002 (2 years before a leap year) 11, 6, 5, 6 and then back to 11. The same pattern occurs with a different starting point, depending where you start in relation to a leap year happening.
So:
| leap year | 6 | 11 | 6 | 5 |
| leap year + 1 | 6 | 5 | 6 | 11 |
| leap year + 2 | 11 | 6 | 5 | 6 |
| leap year + 3 | 5 | 6 | 11 | 6 |
The numbers in each of the rows add to 28 years. So, there will be four of the same day on the same date in every group of 28 years. As there are 7 days in a week and 4 full weeks in a month and 7 x 4 = 28, this proves that my answer is right.
Now, who is going to argue with that!!
Thank you to all readers, including Tim , who sent in solutions to this problem.
