Battery modelling
Find out how to model a battery mathematically
Problem
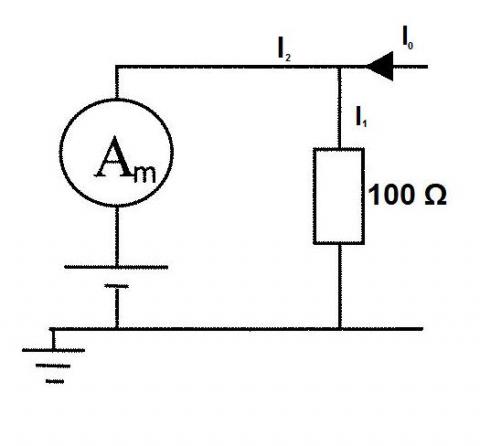
A battery is modelled as a $24\mathrm{V}$ EMF in series with an internal resistance of $2\Omega$. The battery is being charged by a constant current source as shown in the network below. The ammeter, used to measure the current through the battery, has a voltage drop of $2\mathrm{V}$ at full range scales. Here it is set to a $20\mathrm{A}$ range and reads a current of $2\mathrm{A}$.
What is the value of the constant current supplied?
What fraction of the input power is supplied to the battery?
What current would flow into the battery if we now replaced the ammeter with a wire of zero impedance?
Image

Getting Started
Kirchoff's current law states that the sum of the currents into a node are equal to the currents exiting.
Kirchoff's voltage law states that the sum of the voltages around a closed loop equals zero.
Student Solutions
Image
Part 1:
The ammeter will drop a voltage of 2V at 20A, it can therefore be modelled as a resistor of 0.1$\Omega$.
The $100\Omega$ resistor is in parallel with the series combination of the ammeter and battery.
$100 I_1 = (0.1x2) + (2x2) + 24$
$I_1 = 0.282 A$
Current Conservation:
$I_0 = I_1 + I_2$
$I_0 = 2 + 0.282 = 2.282 A$
Part 2:
Power supplied = Power consumed
Power Supplied = $ (0.282^2 x100) + (2^2 x 0.1) + (2x2^2) + (2x24)$ = 64.35 W
Power dissipated by battery = IV = 2 x 24 = 48W
74.6 % of the power supllied is fed into the battery.
Part 3:
$I_0$ is unchanged, $I_0$ = 2.282A
Current conservation:
$I_0 = I_1 + I_2$
Voltage Conservation:
$100 I_1 = 24 + 2I_2 $
Solving these two equations simultaneously we find $I_2 = \frac{I_0 - 0.24}{1.02} = 2.002 A$
