A Circuit Problem
Explore the voltages and currents in this interesting circuit configuration.
Problem
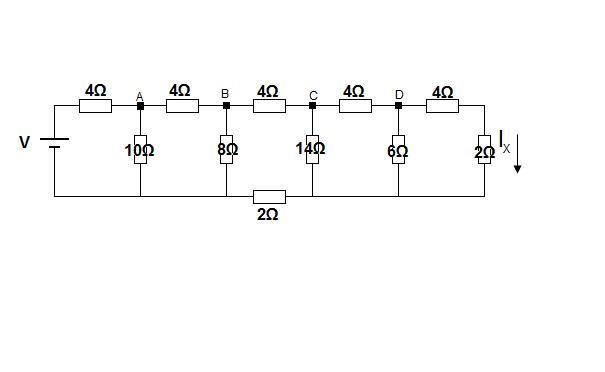
In the circuit shown below, find the current labelled $I_x$ when V = 14 V.
Extensions:
If mesh current analysis is used to to solve this problem, how many unknown currents are there in the circuit? How many simultaneous equations will you end up with?
If nodal voltage analysis is used to solve the problem, what is the minimum number of unknown voltages that would need to be added to the diagram?
Can you think of any ways in which the central branch of the circuit could be simplified without affecting the current $I_x$?
Could you solve this problem using Thevenin and Norton's theorems?
Image
Getting Started
Starting at the right hand side of the circuit, assume a current of
1A flows in resistor X, and work out the potential drops back to
the voltage source. Then use scaling.
Student Solutions
Starting at the right hand side of the circuit, assume a current of 1A flows in resistor X, and work out the potential drops back to the voltage source. Then use scaling.
Let $I_x$ = 1 amp and find the corresponding V.
We can then use scaling to find $I_x$ when V = 14V.
Image

Working right to left:
$I_x$= 1
Find the voltage at d
$V_d = I_x ( 4 + 2) $ = 6V
Find the voltage at c
$V_c = V_d + V_{cd} = V_d + 4I_{cd}$ (Kirchoff's voltage law)
$I_{cd} = I_{d} + I_{x}$ = $\frac{V_d}{6} + 1 = 2$ (Kirchoff's current law)
$V_c = 6V + 8V = 14V $
Find the voltage at b
$V_b= V_c + V_{bc} + (I_x + I_d + I_c)2 $
$I_x = 1$
$I_d = \frac{V_d}{6} = 1$
$I_c = \frac{V_c}{14} = 1$
$I_{bc} = I_c + I_{cd} = 3$(Kirchoff's current law)
$V_b = V_c + 4I_{bc} + 6 $ = $ 14 + 12 + 6 = 32V $(Kirchoff's voltage law)
Find the voltage at a
$V_a = V_b + V_{ab} = V_b + 4I_{ab}$
$I_{ab} = I_{bc} + I_b = 3 + \frac{32}{8} = 7$
$V_a = 32 + 28 = 6OV$
Find V when $I_x = 1$
V = $V_a + 4I_{0a}$
$I_{0a} = I_{ab} + \frac{V_a}{10} = 13A$
$V = 60 + 52 = 112V$
We know that in reality V = 14V
All loads are completely resistive, the relationship between voltage and current is therefore linear.
The current which would have given a voltage of 14 V is therefore 1 x $\frac{14}{112}$= 0.125 A
$I_x$ = 0.125 A
