Electric kettle
Explore the relationship between resistance and temperature
Problem
The diagram shows a simple circuit: the cell provides energy, V volts, which causes a current, I amps, to flow around the circuit. There is also a resistance, R ohms.
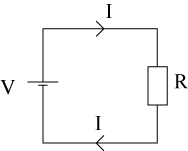
This circuit provides a simple model for what happens in an electric kettle: a resistance converts electrical energy into heat energy by impeding the flow of electrons around the circuit.
The table shows data collected from a circuit like this.
| Resistance (ohms) | Temperature (degrees Celsius) |
| 5 | 44.9 |
| 6 | 50 |
| 7 | 55.1 |
| 8 | 59.9 |
| 9 | 65 |
| 10 | 70.1 |
- Draw a graph of this data, with the resistance on the horizontal axis, putting a straight line through the points.
- Find the gradient of the line.
- Find the equation of the line.
Once you have found the equation, discuss these questions:
- What resistance would you need to heat water to 100 C °?
- What would the temperature be if the resistance was zero?
- Do you think that in practice, any circuit can have zero resistance?
Student Solutions
The equation of the line is $T = 5R +20$, so your gradient should be close to 5.
To heat water to 100 C you need $R = \frac{100 - 20}{5} = 16$ ohms. If the resistance is zero then $T = 20$C. In practice it is really hard to have a circuit with zero resistance. You need special conditions such as a low temperature.
Teachers' Resources
It is not envisaged that this problem would be used as a class problem. It is more appropriate for an enthusiastic student or small group of students looking for a challenge to work on independently.
