Fraction lengths
Can you find combinations of strips of paper which equal the length of the black strip? If the length of the black is 1, how could you write the sum of the strips?
Problem
Here are some lengths, which could be made out of connecting cubes or strips of coloured paper/card:
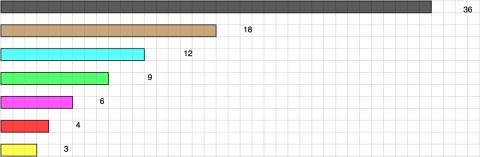
To start with, the black will be counted as ONE so that the brown one is $\frac{1}{2}$, the blue one is $\frac{1}{3}$, etc.
Using different combinations, put them together to equal the length of the black, which is 36 long.
For example, if you were to choose the brown, blue and magenta (pink) you could write them down as the $\frac{1}{2}$, $\frac{1}{3}$, $\frac{1}{6}$
So we would have: $\frac{1}{2} + \frac{1}{3} + \frac{1}{6} = 1$
MOVING ON
Choose any four of the strips, except the black one, and put them together.
Now, compare them with the black.
Here are two examples to start you off. Have a go and find as many different fours as you can.
Using a 3, 6, 12 and an 18 makes 1$\frac{1}{12}$
Using two 12s and two 9s makes 1$\frac{1}{6}$
GOING EVEN FURTHER
Now the light blue strip is the ONE (1).
Use the same fours that you chose before but this time, compare them with the light blue strip instead of the black.
Here are the examples used above, but this time compared with a light blue:
Comparing these four to the light blue it makes 3$\frac{1}{4}$
Comparing these four to the light blue it makes 3$\frac{1}{2}$
Now you go ahead with the fours that you have chosen.
Getting Started
Why is what you've chosen true?
Can you think of a way of writing it down? Can it be written a different way?
What is the 'whole'?
Student Solutions
These came in from St Mary's C of E Primary school Chipping Norton
Joanna and Arthur
We drew a picture to help us and it looked like a wonky staircase. When we did it the first time, we used 18(1/2) 12(1/3) 9(1/4) and 6(1/6). We added them together and we got 1 1/4. When we compared it to the light blue; we got 3 1/4, so the second answer was 2 more than the first.
Cadence
When I compared the blue results with the black results I found out that the answers for blue were three times the answers for black. This due to blue being three times smaller than the black meaning that every fraction that only went into black only once would go into the blue three times more. This is the same for brown. Because brown is half the size of black every fraction that went into black once would go into brown twice. Because green is one quarter the size of black any fraction that went into black once would into green four times. And so on. And that is the answer to another Nrich puzzle. Thank you for reading.
Kaya
I found that, when Incompared my answers for the blue and black strips, they were fairly similar. The answer for he blue strip was three times bigger than the answer for the black strip. This was due to the blue strip being three times smaller, so it went into one more times. For example, brown would be two times bigger than black, due to it being two times smaller. This puzzle was quite challenging at first, but soon became easy when I found out this rule. I really enjoyed taking part in this challenge, and Thank You for reading.
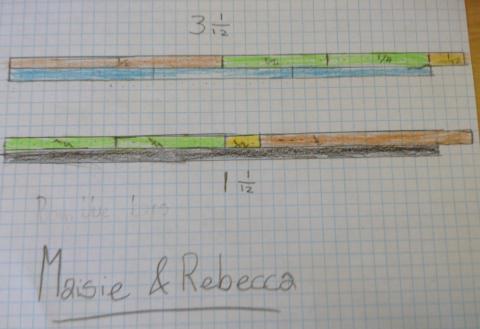
Maisie and Rebecca
We found that with our solution (2 quarters, a half and a twelfth) that with the blue bar it made 3 and 1 twelfth and with the black it made 1 and a twelfth.
When I was looking at the the black stnip I noticed that it was equal to one whole and that it was 36 squares long. Then I looked at the red block or number 4, I thought to myself that 4 is a multiple of 36 because it goes into it 9 times, you could put four red blocks which would be equal to 36, because 4 times 9 equals 36. Another one I found was that the brown stnip is worth 18, if' you know what half of 36 is then you will know that 18 is half, therefore if 18 is half and the brown stn'p is worth 18 then two of those stnips ought to be equal to 36. you can also use two greens, because 9 + 9 = 18 and like I said before 18 is half of the black strip, so two greens is equal to 18 plus 3 more pinks which equals 18 you would get 18 + 18 = 36. Last but not least, 2 twelves, because if 1 twelve fits half the black stnip then 2 is equal to 36.
Now we are using 3 light blue strips for the whole. It says to choose four stnips, so I will chose yellow, green, pink, and brown. So now when I compare them to the three light blue stnips it is not equal to the three light blue strips it is less. So now I will be trying yellow, green, light blue, and brown. My result is that this time it still not equal to the three light blue stnips infact it is going over by 5 squares. This time I will use brown. "9'" blue, green, pink the outcome is that I still can 't get them to equal the three light blue strips.
That's a really good explanation. Thank you for sharing where you got to with the second part. Can anyone help Ryanne?
Thank you for all these submitted solutions keep looking at other Nrich activities.
Teachers' Resources
Fraction Lengths
Here are some lengths, which could be made out of connecting cubes or strips of coloured paper/card:
To start with, the black will be counted as ONE so that the brown one is $\frac{1}{2}$, the blue one is $\frac{1}{3}$, etc.
Using different combinations, put them together to equal the length of the black, which is 36 long.
For example, if you were to choose the brown, blue and magenta (pink) you could write them down as the $\frac{1}{2}$, $\frac{1}{3}$, $\frac{1}{6}$
So we would have: $\frac{1}{2} + \frac{1}{3} + \frac{1}{6} = 1$
MOVING ON
Choose any four of the strips, except the black one, and put them together.
Now, compare them with the black.
Here are two examples to start you off. Have a go and find as many different fours as you can.
Using a 3, 6, 12 and an 18 makes 1$\frac{1}{12}$
Using two 12s and two 9s makes 1$\frac{1}{6}$
GOING EVEN FURTHER
Now the light blue strip is the ONE (1).
Use the same fours that you chose before but this time, compare them with the light blue strip instead of the black.
Here are the examples used above, but this time compared with a light blue:
Comparing these four to the light blue it makes 3$\frac{1}{4}$
Comparing these four to the light blue it makes 3$\frac{1}{2}$
Now you go ahead with the fours that you have chosen.
Why do this problem?
This activity gives the opportunity for meaningful discussion as learners find solutions so they will be deepening their understanding of the concept of fractions and becoming acquainted with relationships between fractions. This activity also involves addition of fractions with different denominators and mixed numbers, so that the concept of equivalent fractions is also explored. As children tackle this task, it will be very important to repeatedly draw their attention to what is the "one".
Possible approach
This activity can be introduced by showing the image on an IWB. To begin with, you could say very little apart from asking the children what they notice or what they see. This provides a non-threatening environment in which they can talk to a partner first and then share their 'noticings' with the wider group.
You could then introduce the first task. Groups of pupils should have use of connecting cubes or strips of paper (till roll paper works well) or whatever is available to match the shown lengths.
There may be disagreements between different groups and this can lead to a healthy discussion as each group tries to justify their suggestions. Try to step back as much as possible during this kind of discussion and remain a facilitator, so that the children look to each other for explanations, rather than straight to you.
Key questions
Why is what you've chosen true?
Can you think of a way of writing that down? Can that be written a different way?
Tell me about your choice of fractions.
Possible extension
If a group or individual pupil has successfully completed the third part of the task, then ask them to look at each fraction and relate it to the other sizes, for example:
The 6 is $\frac{1}{6}$ if the 36 is 1 whole
and is $\frac{1}{3}$ if the 18 is 1 whole
and is $\frac{1}{2}$ if the 12 is 1 whole
and is $\frac{2}{3}$ if the 9 is 1 whole
and is 1$\frac{1}{2}$ if the 4 is 1 whole
and is 2 if the 3 is 1 whole
You could also encourage similar comparisons when the compared length is not a whole 1 but, for example, $\frac{2}{3}$:
The 6 is $\frac{1}{9}$ if the 36 is $\frac{2}{3}$
and is $\frac{2}{9}$ if the 18 is $\frac{2}{3}$
and is $\frac{1}{3}$ if the 12 is $\frac{2}{3}$
and is $\frac{4}{9}$ if the 9 is $\frac{2}{3}$
and is 1 if the 4 is $\frac{2}{3}$
Possible support
Some pupils may need reminding that the 36 is a whole 1 one all the time in the first part of the task.