Warmsnug Double Glazing
Problem
Warmsnug Double Glazing printable worksheet
Warmsnug calculate the prices of their windows according to the area of glass used and the length of frame needed.
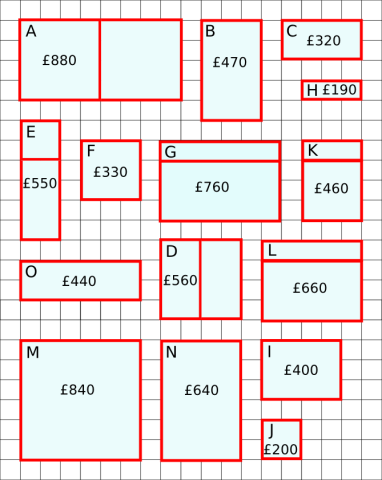
Can you work out how Warmsnug arrived at the prices of the windows below?
Which window has been given an incorrect price?
This spreadsheet generates prices for the windows according to different pricing rules.
Can you find an efficient strategy for finding how the prices were calculated?
Getting Started
Start by looking at the windows with only one pane.
Are there any windows that use the same amount of glass?
How do their frame lengths differ?
Are there any windows that use the same amount of frame?
How do their glass areas differ?
Click to reveal a handy table with the areas and frame lengths of all the windows:
| Length of frame |
Area | Cost | |
| A | 28 | 32 | £880 |
| B | 16 | 15 | £470 |
| C | 12 | 8 | £320 |
| D | 20 | 16 | £560 |
| E | 18 | 12 | £550 |
| F | 12 | 9 | £330 |
| G | 26 | 24 | £760 |
| H | 8 | 3 | £190 |
| I | 14 | 12 | £400 |
| J | 8 | 4 | £200 |
| K | 17 | 12 | £460 |
| L | 23 | 20 | £660 |
| M | 24 | 36 | £840 |
| N | 20 | 24 | £640 |
| O | 16 | 12 | £440 |
Student Solutions
We looked at K (Area = 12, Frame = 17) and I (Area = 12, Frame = 14) and we used the £60 price difference to find out the cost of the frame ( £20 per unit) and the cost of the glass ( £10 for each 1 by 1 pane).
Millie and Kate's method for finding the costs of the frame and the glass is very neat:
K had 3 cm of extra frame and was £60 more so we divided it by 3 to find that each centimetre of frame was £20.
Similarly, Jake from Colyton Grammar School started by finding the price of each unit square of glass:
J (Area = 4, Frame = 8) and H (Area = 3, Frame = 8) each have the same length of frame, but J has one square of glass more. J costs £10 more than H so that means that a 1 by 1 pane of glass costs £10.
Once these prices have been found, the correct price of each shape can be found and compared to its price tag. But what would happen if one of K, I, J or H had the wrong price tag? Would this method work? Luckily, many students checked all the price tags and found that the only incorrect one is E.
E has 18 frame squares and 12 glass panes, so it should cost £360 + £120, which equals £480. The price marked is £550, so window E is wrong.
Rhea from Loughborough High School used a very systematic approach to make sure she found the window that was priced incorrectly. She used an algebraic method with simultaneuous equations:
I used X to represent the price of the frame per square and Y to represent the price of the glass per square. For each window I wrote an equation using X and Y:
A. 28X + 32Y = £880 (The frame borders 28 squares and the area of the glass is 32 squares)
B. 16X + 15Y = £470 (The frame borders 16 squares and the area of the glass is 15 squares)
C. 12X + 8Y = £320 (etc.)
D. 20X + 16Y = £560
E. 18X + 12Y = £550
F. 12X + 9Y = £330
G. 26X + 24Y = £760
H. 8X + 3Y = £190
I. 14X + 12Y = £400
J. 8X + 4Y = £200
K. 17X + 12Y = £460
L. 23X + 20Y = £660
M. 24X + 36Y = £840
N. 20X + 24Y = £640
O. 16X + 12Y = £440
I then looked for equations which had equal X or Y figures. I used these
equations to explore some simultaneous equations:
F. 12X + 9Y = 330
C. 12X + 8Y = 320
F - C:
Y = 10
J. 8X + 4Y = 200
H. 8X + 3Y = 190
J - H:
Y = 10
N. 20X + 24Y = 640
D. 20X + 16Y = 560
N - D:
8Y = 80
Y = 10
B. 16X + 15Y = 470
O. 16X + 12Y = 440
B - O:
3Y = 30
Y = 10
As all the answers to the simultaneous equations which I investigated are Y = 10, and there is only one incorrect equation, Y must equal £10.
It also indicates that equations (and the prices of) F, C, J, H, N, D, B and O must be correct.
G. 26X + 24Y = 760
N. 20X + 24Y = 640
G - N:
6X = 120
X = 20
K. 17X + 12Y = 460
I. 14X + 12Y = 400
K - I:
3X = 60
X = 20
E. 18X + 12Y = 550
M. 24X + 36Y = 840
M/3. 8X + 12Y = 280
E - M/3:
10X = 270
X = 27
C. 12X + 8Y = 320
D. 20X + 16Y= 560
D/2. 10X + 8Y = 280
C - D/2:
2X = 40
X = 20
As 3 out of 4 of the answers to the simultaneous equations investigated are X = 20, I assume that X must £20.
It also indicates that either equation (and the prices of) E or M is the incorrect one because when they are solved in a simultaneous equation, they produce a different answer to all the others.
Let X= £20 and Y= £10
I entered these values into all the equations to see if they fitted in with the figures.
All of them except E proved to be correct:
E. 18X + 12Y = 360 + 120 = 480; so the price for window E is incorrect.
This makes sense because E didn't produce the right answer when put in a simultaneous equation.
Well done to everyone who found the solution.
Can you see the similarity between the algebraic method and the 'comparing pairs' method?
Teachers' Resources
Why do this problem?
This problem is ideal for considering the variety of methods of generating and solving simultaneous equations within the context of calculating areas and perimeters of rectangles.
Mathematics lessons can sometimes feel neatly packaged, with information, techniques, patterns all readily accessible. But what do we do when the information arrives all jumbled up (with occasional errors) and we're asked to make sense of it? The problem offers students a chance to develop strategies for organising and understanding such situations.
Possible approach
Project this image of the windows.
"Imagine you are the owner of a double glazing business. What variables do you think you would need to consider when deciding on the prices for your windows?"
Collect together ideas of the possible relevant variables.
"Warmsnug Double Glazing price their windows according to the area of glass used and the length of frame needed. Here is a worksheet showing the prices of different sized windows. Can you work out how Warmsnug arrived at the prices of these windows? Watch out - one of the windows has been priced incorrectly!"
Give students time to work together. While they are working, circulate and listen out for useful insights. If students are stuck, here are some helpful prompts:
- Are there any windows that use the same amount of glass?
How do their frame lengths differ? - Are there any windows that use the same amount of frame?
How do their glass areas differ?
Once students think they have found a solution, challenge them to find a few different strategies for arriving at the pricing structure.
Give students time to work on this in pairs. While they are working, circulate and listen out for useful insights.
This worksheet has all the relevant data along with some efficient methods for finding the pricing structure. If your focus is on solving simultaneous equations give the class plenty of time to find as many different ways of finding the pricing structure as they can.
Bring the class together to share the new methods they have devised.
Next, hand out worksheet 1, worksheet 2, and worksheet 3, which become progressively more demanding. The problems on these sheets offer students the opportunity to apply and refine the methods they shared
for the initial problem.
Alternatively, if a computer room is available students can work on this spreadsheet version.
Finally, use the spreadsheet to generate a Level 1, 2 or 3 problem and challenge the class to use an efficient method to work out the pricing structure and the incorrectly priced window.
Possible support
Along with the prompts above, suggest to students who are struggling with the large quantities of information that they initially ignore the windows with two panes.
Possible extension
For a follow-up problem on area and perimeter, see Changing Areas, Changing Perimeters.