Usually, we invite students to send us their solutions to a selection of problems, but this December and January we are doing things a little differently…
The problems below contain interactivities which offer students instant feedback, and we think they are particularly suitable to work on at home, perhaps with a family member, during the holiday period. We hope you enjoy the challenges we’ve selected.
Live problems
-
problemFavouriteFruity totals
Age7 to 16Challenge level
In this interactivity each fruit has a hidden value. Can you deduce what each one is worth?
-
problemFavouriteDozens
Age7 to 14Challenge level
Can you select the missing digit(s) to find the largest multiple?
-
problemFavouriteHave you got it?
Age11 to 14Challenge level
Can you explain the strategy for winning this game with any target?
-
problemFavouriteConnect three
Age11 to 16Challenge level
In this game the winner is the first to complete a row of three. Are some squares easier to land on than others?
-
problemCrossing the bridge
Age11 to 18Challenge level
Four friends must cross a bridge. How can they all cross it in just 17 minutes?
Recently solved problems
-
problemFavouritePicturing square numbers
Age11 to 14Challenge level
Square numbers can be represented as the sum of consecutive odd numbers. What is the sum of 1 + 3 + ..... + 149 + 151 + 153?
-
problemFavouriteCuboid challenge
Age11 to 16Challenge level
What's the largest volume of box you can make from a square of paper?
-
problemFavouriteSlick summing
Age14 to 16Challenge level
Watch the video to see how Charlie works out the sum. Can you adapt his method?
-
problemFavouriteQuadratic patterns
Age14 to 16Challenge level
Surprising numerical patterns can be explained using algebra and diagrams...
-
problemFavouriteCharlie's delightful machine
Age11 to 16Challenge level
Here is a machine with four coloured lights. Can you develop a strategy to work out the rules controlling each light?
-
problemFavouriteM, M and M
Age11 to 14Challenge level
If you are given the mean, median and mode of five positive whole numbers, can you find the numbers?
-
problemFavouriteCyclic quadrilaterals
Age11 to 16Challenge level
Draw some quadrilaterals on a 9-point circle and work out the angles. Is there a theorem?
-
problemFavouriteTilted squares
Age11 to 14Challenge level
It's easy to work out the areas of most squares that we meet, but what if they were tilted?
-
problemFavouriteTake three from five
Age11 to 16Challenge level
Caroline and James pick sets of five numbers. Charlie tries to find three that add together to make a multiple of three. Can they stop him?
-
problemFavouriteAdd to 200
Age11 to 14Challenge level
By selecting digits for an addition grid, what targets can you make? -
problemFavouriteWipeout
Age11 to 16Challenge level
Can you do a little mathematical detective work to figure out which number has been wiped out? -
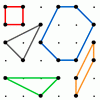problemFavouritePick's theorem
Age14 to 16Challenge level
Polygons drawn on square dotty paper have dots on their perimeter (p) and often internal (i) ones as well. Find a relationship between p, i and the area of the polygons.