Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Haringey Leadership for Learning Project 2015-16
From December 2015 to May 2016, NRICH is working on a project with Haringey Council, for primary maths subject leaders in the borough, entitled 'Leadership for Learning'. The project comprises four face-to-face days and linked 'gap' tasks.
We hope that, by the end of the project, participants will have:
- a vision for the place and purpose of mathematics in the primary curriculum
- a deeper understanding of what it might mean to be 'mastering mathematics'
- the ability to effect leadership change.
Liz Woodham, one of the NRICH Primary Coordinators, is leading the project with Michael Hall, an independent consultant, who has worked with Liz on previous projects in Haringey.
This page summarises the content and discussions during each day. If you have any queries about the project, please contact the primary NRICH team.
Day 1: Wednesday 2 December 2015
Agenda.docx
pdf of PowerPoint slides used
The aims of Day 1 in particular were:
- To explore ways of integrating problem solving into the primary mathematics curriculum
- To consider how to support colleagues in develping appropriate strategies for problem solving in their classrooms.
We began with a discussion after Michael posed the question, "How important is it for children to learn their tables?" Points made included:
- Important for the test, but not for real life
- It's useful for speed and efficiency but it's not the end of the world if children don't know them all by heart
- It's more important to know what multiplication means and how to work it out
- Being good at tables seems to be associated with being a good mathematician, but that's not true.
Michael set us off on the first task in session 1 by asking us to write consecutive multiples of 7, each on a single sheet of paper, so that there weren't any repetitions. He then invited us to stand up holding one of the sheets and arrange ourselves in order. In the picture below, we are standing from 0 on the left to 56 on the right:

He then paired us so that 0 went with 56, 7 went with 49, 14 with 42 etc.and this left 28 without a partner:

We noticed that the sum of each pair of numbers (or double 28) was the same - 56. Why? We explored this in pairs and Michael invited us to say what we had been doing, which resulted in this list:

MIchael suggested that we think about this activity more before next time and bring back ideas to share.
Liz introduced seven aspects to consider if we want to embed problem solving into the curriculum (problem solving 'unpacked') - see the pdf of the PowerPoint slides linked above for details. We had a go at Totality and discussed its characteristics as a low threshold high ceiling (LTHC) task. Liz then showed us the image in Baravelle and after discussing what we
saw, the challenge was to recreate it. This led to a discussion about rich tasks. Liz explained that tasks on the NRICH site are rich and some of them are LTHC.
We discussed the seven key problem-solving skills which NRICH believes children need to have at their fingertips (again see the PowerPoint slides). We had used all of them in one of both of the two tasks we had tried.
In session 2, we each considered the strengths in terms of mathematics and problem solving in our own schools along with the challenges we face. Some of the issues that came up were:
- curriculum overload (Michael suggested that not all the the curriculum objectives are equally important so perhaps it's useful to identify the most important and think about their progression)
- mismatch between test papers and the curriculum aims
- the difficulty of assessing and evidencing problem-solving skills and reasoning
- what should maths books look like?
- children need a good working memory
Here are photos of the flipchart notes each table made:



Michael and Liz promised to think about these issues and try to begin to address them in future days.
Session 3 continued to 'unpack' problem solving. We considered types of tasks (finding all possibilities, visual, logic, rules and patterns, word problems) and how to structure the problem-solving process by having a go at Dicey Addition. We began by playing the game competitvely in pairs or threes and talked about what we were attending to.
We then had the same four numbers to place in the calculation so that we could prove our own arrangement was the closest possible to 100.
We also discussed learning objectives - it is important to have objectives which not only focus on curriculum 'content', but also on problem-solving skills and the problem-solving process.
After lunch in session 4, Michael introduced us to the 'knowledge quartet' (see pdf of PowerPoint slides) as a possible framework when we observe colleagues teaching. (It has been developed by researchers in the Faculty of Education at Cambridge University.) We watched a lesson on fractions and used the knowledge quartet
to reflect on practice. The following comments were made:
- The level of questioning needs to be increased
- The teacher could have drawn attention to different representations more effectively
- The lesson needed more challenge throughout
- There was too much demonstration
- The word 'equals' was missing.
We felt that teachers need to be brave to steer away from the lesson plan and may not have the subject knowledge to do so effectively.
One delegate described how she felt very lucky in her school as they were encouraged to experiment with maths. The headteacher and maths subject leader are very supportive, having been on NRICH CPD and mastery training. They focus on the learning journey rather than answers, and have a growth mindset philosophy.
Michael then led us in some counting stick activities. We threw a dice to get the starting number and again for the step size. Michael asked:
- Is there a pattern?
- What step size/starting number would make the pattern easier?
This led on to counting remainders when dividing by 4 using the stick which led to 0, 1, 2, 3, 0, 1, 2, 3, 0 ... We discussed that visual clues would be useful here so we didn't have to remember what number we were on before doing the division (cards with arrows on would work).
We then watched a teacher counting in fractional steps with a Year 2 class: http://vimeo.com/83486101. We noted how the rhythm helped and how the children were developing their vocabulary, for example some said "three and one quarter" rather than the more commonly used 'three and a quarter". Michael challenged everyone to
have a go at a counting stick activity in their own class and to encourage every year group in the school to try a suitable counting task with the stick as well.
Before giving everyone some time to plan what to take back to school, Michael led another task. He invited delegates to give him a number which he then wrote on the flipchart and wrote up two more numbers next to it. He repeated this several times and we noticed that each set comprised three consecutive numbers. He then wrote the sum of each set of three numbers next to the set:

We noticed that each sum as a multiple of 3. Why? This led to discussing use of manipulatives to create a visual proof and an algebraic proof too:
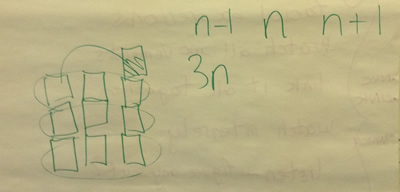
In the final session of the day, after allowing some time for participants to plan what to take back to school, we focused on the last two aspects to 'unpack' problem solving, namely recording and classroom culture. We looked back at all the recording we had made as we had worked on the tasks today and discussed what it looked like and its purpose. Liz drew attention
to the Recording Feature which focuses on three different purposes for recording (see also the PowerPoint slides linked above).
We finished the day by discussing the kind of mathematical behaviours we value and encourage in our classrooms (see also the PowerPoint slides).
Expectations for Day 2 (Wednesday 3 February)
We agreed to work on the following before next time:
- Consider the multiples of 7 task described above in session 1 and come prepared to explain why each pair of numbers has the same total
- Try out a counting stick task with our own classes and encourage all other teachers in school to do the same
- Try out any other tasks from today and feed back (including anecdotes)
- Think about ideas for staff meetings to share.
Day 2: Wednesday 3 February
Agenda.docx
pdf of PowerPoint slides used
The aims of Day 2 in particular were to:
- Look at progression in reasoning
- Discuss ways of helping children get better at communicating reasoning
- Consider how to support colleagues in developing reasoning in their classrooms.
We began session 1 with a challenge given by Michael:
Multiply it by 10
Take away the number you first thought of
Multiply by 7
Double
Double again
Double again
Double again
Dougle again
Divide by the number you first thought of
Happy new year!
We realised that we had all got 2016 as our answer. Why? Michael offered a clue that factors might be important. Having discussed ideas on our tables, we shared thoughts with the whole group and Michael jotted the following:
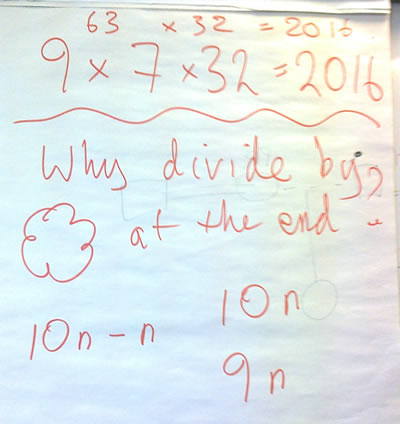
After more discussion, we were able to reason through to a solution:
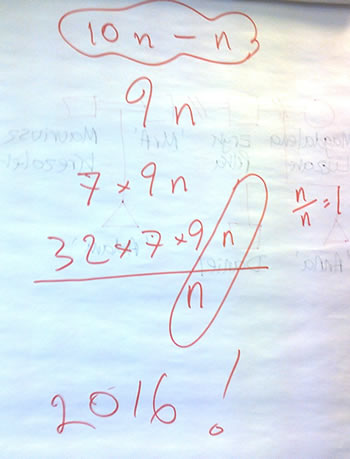
Michael then introduced the idea of a 'light touch' reasoning challenge: if there are two ducks in front and two ducks behind, how many ducks are there? We were invited to draw the ducks:
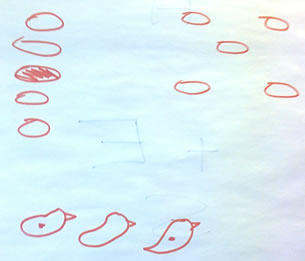
We decided there could be three or five ducks, depending on whether the number of ducks in front and behind were both from the point of view of the same duck or not. In the case of five ducks, we found two possible arrangements.
Another example of 'light touch' reasoning could be something like:
We thought there must be at least nine, but if they were all different there might be 16. But then we wondered whether we had seen them all ...
Liz mentioned the idea of 'odd one out' which is a great context in which to encourage children to begin to reason. For example, you give three numbers and children are asked which is the odd one out and why; then to choose another to be the odd one out and state why; and then state why the third number could be the odd one out.
Liz led session 2 by introducing the Largest Even task. We were challenged to generalise our strategy and to decide how it would change if we used the digits 0-9 rather than 1-9 as we had done initially. Liz outlined NRICH's ideas about the five step progression in reasoning:
- describing
- explaining
- convincing
- justifying
- proving
(See our article Reasoning: the Journey from Novice to Expert for further details about each step in the reasoning journey.) We talked about this progression in the context of Largest Even.
In session 3, participants discussed their experiences so far in schools, including reporting back on any tasks from last time that they (and colleagues) had tried with learners. Each table produced a poster of key points:



Liz continued to delve into progression in reasoning during session 4 through the Square Subtraction task on NRICH. We discovered that we always got an odd answer and Liz asked everyone to try to work out why, perhaps by drawing a picture. These were three different solutions:
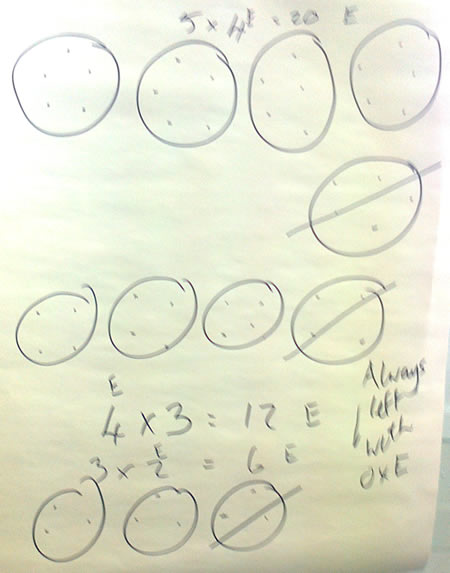


We discussed how, with some additional written or spoken explanation, any of the above three solutions would constitute a proof, the highest 'level' on the reasoning journey. Liz delved into proof a bit further, outlining how we might usefully consider ways of communicating/recording proof as well as methods for proving (see slide 10 of the above presentation). We concluded that
Square Subtraction lends itself to visual and algebraic ways of communicating/recording proof.
After lunch, Michael led another task. He asked us to enter a three-digit number into a calculator, then to make a six-digit number by repeating the three digits. For example if I chose 347 as my three-digit number, I would then have 347 347 as my six-digit number. We discussed a few questions that Michael posed:
If you divided by 2, what would you get? [half, smaller, even/odd ...]
If you divided by 3, what would you get? [less chance of gettng a whole number?]
If you divided by 4, what would you get?
If you divided by 5, what would you get?
If you divided by 6, what would you get?
Then Michael asked us what we thought would happen if we divided our six-digit number by 7 and invited us to actually do this on the calculator. We got a whole number! And if we divided that resulting number by 11, we also got a whole number. Then dividing the resulting number by 13 also gave everyone a whole number, which was surprising! We were challenged to work out
why this is the case ...
In session 6, Liz introduced the game Five Steps to 50 which lends itself to discussing all the five steps in the reasoning journey. We talked about five methods for proving which might be appropriate for primary aged children:
- Proof by contradiction (e.g. Make 37)
- Proof by counter example (e.g. Five Steps to 50)
- Generic proof (e.g. Three Neighbours - summing three consecutive numbers which we tried on Day 1)
- Proof by exhaustion (e.g. Dicey Addition which we also tried on Day 1)
- Proof by logical reasoning (e.g. Largest Even)
For further details about each of these, see our article Mastering Mathematics: the Challenge of Generalising and Proof.
Liz then went on to share NRICH's thinking about how we can help children get better at communicating their reasoning (see slide 14 of the pdf linked above). We tried Lots of Lollies and then Liz gave out some cards which contained some children's ways of approaching the task (these are provided in the Teachers' Resources section of the
task). We were invited to choose one way and continue the method to a full solution. This involved having to understand how others have worked, without being able to ask them directly about what they have done, which can be a powerful way to help children get better at communicating reasoning.
We then watched the video of Jill Mansergh on YouTube using the counting stick to learn the 17 times table. We discussed the ways in which Jill elicits reasoning, which includes general strategies for making learners feel at ease as well as using mathematical questions and prompts which encourage reasoning.
Delegates had time during the afternoon to consider whether they might lead a staff meeting or series of staff meetings using these days as a stimulus and we heard from some who had already begun this process. The day finished with a short time for planning what to try out back at school before our next day together.
Expectations for Day 3 (Wednesday 9 March)
We agreed to work on the following before next time:
- Try out any tasks from today and feed back (including anecdotes)
- Continue to think about ideas for staff meetings or how to follow up from the staff meeting/s already led.
Day 3: Wednesday 9 March
20160309Agenda.docx
pdf of PowerPoint slides used
The aims of Day 3 in particular were to:
- deepen our own understanding of what is meant by 'fluency'
- discuss how we can help children become more fluent in mathematics
- consider how to support colleagues in developing fluency in their classrooms.
To begin, Michael reminded us that 14 March is Pi Day (written in the American format the date is 3.14 which makes the first three digits of pi) and he mentioned a website which had some nice ideas about how to celebrate, including making a pi skyline from Cuisenaire rods (see here).
Session 1 kicked off with Michael posing the following challenge:
Think of three consecutive whole numbers.
Find the product of the outer two.
Square the inner one.
Find the difference between these two answers.
What do you notice?
We found that the difference always seemed to be 1 and we tried to explain why. One member of the group proved (by exhaustion) that it was always the case for single digit consecutive numbers. Some of us found an algebraic solution and Michael also demonstrated a pictorial proof:
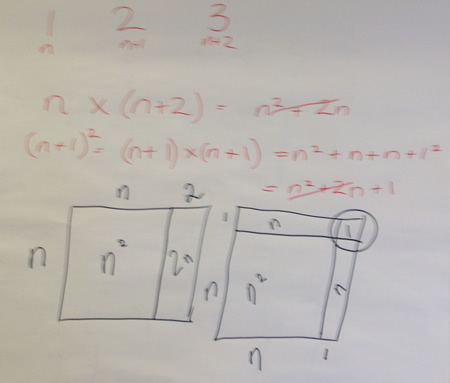
We discussed the value of an activity like this and the following suggestions were shared:
- practising multiplication
- using different terminology
- looking for patterns
- conjecturing
- exploring and discovering
This led into a discussion about fluency being more than a measure of speed. Michael drew attention to the difference between 'know from memory' and 'memorisation'. He suggested that this kind of activity 'subordinates' table facts, in other words knowing multiplication facts is useful for this task but they are not the driver.
We also began to ask our own questions, such as what happens for four/five/six ... consecutive numbers? For four consecutive numbers, we found the product of the outer two and the product of the inner two, then found the difference between those two answers. This gave us a difference of 2 every time. We wondered how we might get a difference of 3 using five consecutive numbers
and we tried finding the difference between the product of the outer pair and the product of the second and fourth numbers:
n, n+1, n+2, n+3, n+4
Product of outer pair is n(n+4)
Product of second and fourth is (n+1)(n+3)
Difference of these two products is n(n+4) - [(n+1)(n+3)] = n$^2$ + 4n - (n$^2$ +3n +n +3)
= n$^2$ + 4n - n$^2$ - 4n - 3
= -3
Using consecutive numbers starting with 1, we looked briefly at six and seven consecutive numbers and did a similar thing:

So, in the case of numbers 1-6, the product of 1 and 6 is 6; the product of 2 and 5 is 10 so the difference is 4.
In the case of 1-7, the product of 1 and 7 is 7; the product of 2 and 6 is 12 and therefore the difference is 5.
Michael then went on to remind us of one of the Numeracy Strategy's interactive teaching programs (ITPs) which was called 'number grid'. We started with the 1-100 square and coloured all the primes:
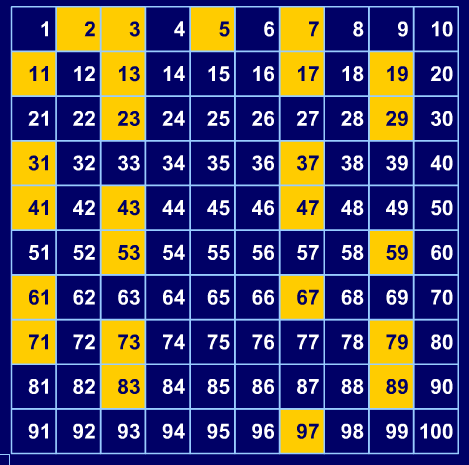
Then we changed the grid size so that it only had nine columns, rather than ten. We noticed that there were no primes in the '6' column or '9' column. Why?

We then reduced the number of columns again to eight. Michael asked us what was the same and what was different. Again, we talked about what we noticed and tried to explain why that pattern occurred.
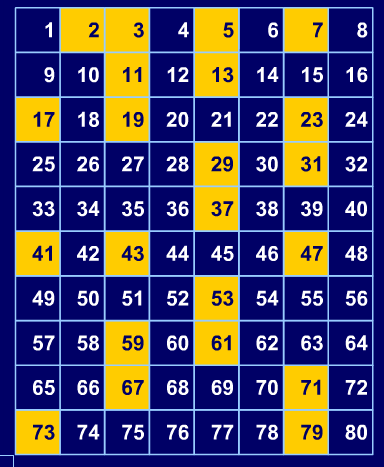
Michael asked us to predict what would happen when we reduced the number of columns to seven. This gave some interesting diagonal patterns which prompted us to notice that lots of pairs of primes have a difference of 6. We also noticed that all columns had primes.
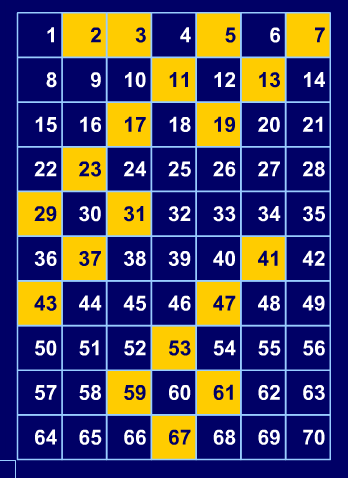
We tried to predict what might happen when the number of columns were reduced to six. This made us all gasp!
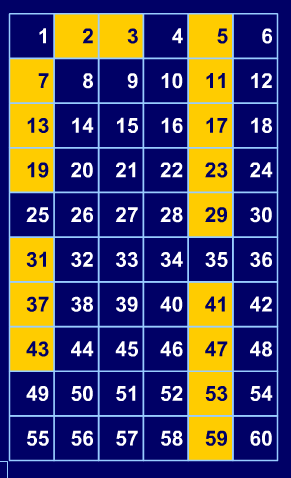
All the primes on the grid (apart from 2 and 3) are either one more or one less than a multiple of six (although it is not always the case that a number one more or one less than a multiple of six is prime). This led into discussing how we might ask children to investigate whether numbers on either side of a multiple of six are prime or not.
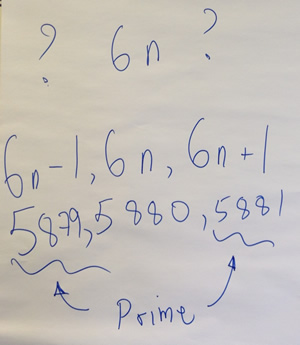
One participant mentioned a teacher on Twitter, Rob Carpenter (@carpenter_rob), who tweets nice examples of stimulating envirnoments a bit like this series of questions about primes on the number grid.
In session 2, Liz invited participants to reflect on their own understanding of what fluency might mean before we had a go at Spiralling Decimals. We thought about the following four questions in relation to this game:
- What is the mathematical knowledge that is needed to play?
- Who would this game be for?
- What is the 'value added' of playing the game for high-attaining/low-attaining children?
- How could you adapt this game to use it in your classroom?
This led us to tweak our own definitions of fluency and chat to others about how theirs compared with ours.
In session 3, delegates discussed their experiences of using rich tasks back at school since the last day together. Here are some of the key points:

Other comments included:
- Mastery is not about speed. It is about reasoning and problem solving to develop fluency.
- There is a significant difference between 'investigations' and 'working investigatively'. The latter is to aim for.
- Reasoning/generalising needs to happen all the time, not as the focus for some lessons.
- Reasoning needs modelling.
- In the moment - use what they (learners) say.
- Written communication of ideas - displayed (to see/refer to over time)
- Finding a way in to a task matters (e.g. in terms of motivation and engagement) - pictures, images, video clips etc.
Liz continued the focus on fluency in session 4, where we began by looking at fluency in the National Curriculum (see pdf of PowerPoint slides above). Liz introduced us to some research on fluency in the context of calculation which was conducted by Susan Russell in the States. She suggests that there are three aspects to fluency: efficiency, accuracy and
flexibility. We also talked about procedural vs conceptual fluency and how both are important.
We had a go at two more NRICH tasks: Playing Incey Wincey Spider and Number Match. We discussed how each task encourages the different aspects of fluency.
After lunch in session 5, Michael gave out sixteen cards, which comprised the following numbers:
1, 1, 2, 2, 2, 3, 4, 5, 5, 6, 8, 8, 8, 10, 11, 14.
The challenge was to put them in some order. Michael gave us a clue that there were three sequences. This led to:
2, 4, 6, 8, 10
1, 1, 2, 3, 5, 8
2, 5, 8, 11, 14
We discussed how we would describe each one and looked at the second one a bit more (this is the Fibonacci sequence where each term is the sum of the two previous ones). We continued it forwards and backwards. We then looked at the ratio of successive terms, which tended towards approximately 0.618. We started with two different numbers and created a sequence in the same way and
investigated the ratio of successive terms again. No matter what the two starting numbers were, the ratio did the same thing, tending towards 0.618. We even investigated starting with two fractions.
Michael talked about the occurrence of Fibonacci numbers and the Fibonacci sprial in nature, and drew attention to Vi Hart's Fibonacci doodle on YouTube.
To finish session 5, Michael invited us to spell 'supercalifragilisticexpialidocious'. He asked us how many letters it has (34) and wrote down:
THIRTY FOUR -> TEN -> THREE -> FIVE -> FOUR -> FOUR -> FOUR ...
Participants realised that each term is the number of letters in the previous word and we explained why the sequence always stops on 'four' no matter what word you begin with. Michael offered a similar task:
1, 11, 21, 1211, 111221, 312211 ...
in which each term refers to the number of different kind of digits in the previous term. So, the second term is 'one 1'; the third is 'one 2, one 1' etc.
In session 6, Liz introduced a number of NRICH tasks and we discussed how each one might encourage children to become more fluent in number and calculation:
Reasoned Rounding - fluency with concepts, flexibility
Factors and Multiples Game - fluency with facts, accuracy and flexibility
Four Go - fluency with calculation strategies, using knowledge in new contexts, accuracy and flexibility
Liz explained that although today we had been discussing fluency in the context of number and calculation, the NRICH team believes fluency is more widely applicable than that. We looked at this sheet, which outlines NRICH's view and links to NRICH tasks which might help encourage learners to be fluent in contexts beyond number and
calculation.
Liz also reminded participants about the NCETM website, which is free of charge but requires users to register. In particular, Liz drew attention to the Primary Magazine, and two sections of it in particular (you'll need to be logged in to view the magazine):
'Seen and Heard' - provides a specific example of a child's response to mathematics in a classroom to stimulate thinking and provoke questions about how you would react to similar events in your own classroom.
The day concluded with some time for delegates to plan what they might try out back at school before our next day together.
Expectations for Day 4 (Wednesday 25 May)
We agreed to work on the following before next time:
- Try out any tasks from today and feed back (including anecdotes)
- Continue to think about ideas for staff meetings or how to follow up from the staff meeting/s already led.
Day 4: Wednesday 25 May
20160525Agenda.docx
pdf of slides used during the day
The aims of day 4 in particular were to:
- deepen our own understanding of what might be meant by 'mastering mathematics'
- discuss how we can help children 'master' mathematics
- consider how to support colleagues in developing mastery in their classrooms.
We started session 1 with a task posed by Michael. He asked one table to choose a three-digit number, which they wrote on the flipchart. He then explained that we would be writing five three-digit numbers altogether and that he already knew what the total was going to be. He wrote this total on a piece of paper which was folded up. He then asked another table to choose a second three-digit number, which they wrote below the first number. Michael then wrote a third three-digit number himself, then the first table wrote another three-digit number and Michael wrote the final three-digit number. Here are the five numbers in the order in which they were written on the flipchart:
139
860
473
526
Michael asked us to find the total and it did indeed match the number which he had written on the paper (2266). How had this been done?
We tried it again with a new set of five three-digit numbers, which turned out to be:
891
108
789
210
Again, Michael correctly predicted the total.
Steph noticed that the second and third numbers added up to 999, and so did the fourth and fifth numbers. Together, we reasoned that we were therefore adding 2 x 999 onto the first number. There were suggestions about how to tweak this task, for example by using a different number of digits or decimals, or by adding 999 more than twice.
We discussed the way the challenge had been introduced - involving us in creating the numbers made it feel more collaborative rather than passive. Michael drew a distinction between a task (which you might find in a book, online etc.) and the activity (i.e. what actually happens in the classroom, which might be unpredictable). In this case, the 'magic' provided a hook which was the
driving force behind the procedural adding.
Michael then introduced us to another task, this time focusing on paper folding (taken from this Association of Teachers of Matheamtics recent publication). Michael began by asking us what we know about A4 paper and then invited us to imagine folding it in half and to describe what
we would see. Then, using paper, we actually folded in half length-ways and opened out; then folded the bottom left corner up to meet the fold line, then the right-hand corner up to meet the left-hand edge. At this point we had a pentagon and finally we folded down the part that 'stuck out' to make a triangle:

But was it an equilateral triangle? We tried to prove that it was, though we found we were having to make assumptions. Michael set us the challenge of trying to prove this in our own time.
We discussed the power of origami in looking at mathematical structures and Michael recommended another Association of Teachers of Mathematics publication: Mathematical Imagery. We also talked about how simply folding A4 a couple of times provides some nice starter tasks by asking questions
such as:
- What angles do you recognise?
- What relationships do you know?
This led into another paper folding task. This time Michael asked us to turn a piece of A4 paper into landscape orientation and fold the top left corner to the bottom, then the top right to meet the edge which had just been folded. What is the resulting shape? We thought it was a kite:

... but the challenge is to prove it. We also discussed the dimensions of A4 paper (sides in the ratio $1:\sqrt 2$) and found the perimeter of a sheet ($2 + 2\sqrt 2$). Michael gave us a challenge to work on in our own time - to find the perimeter of the kite (which needs some Pythagoras' Theorem).
In session 2, Liz asked us to consider what we understood by the phrase 'mastering mathematics'. The following points were mentioned:

Liz emphasised the use of the verb 'masterING' to suggest that this was an ongoing process which didn't have a fixed end point. Liz summarised NRICH's view, that if we are aiming to nurture young mathematicians, then the following five strands might be helpful to bear in mind:
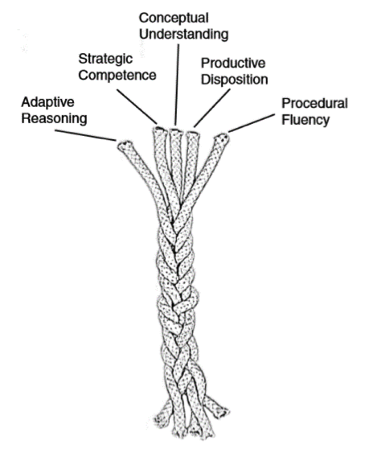
(This model is taken from a book, 'Adding it up: Helping children learn mathematics' by Kilpatrick, Swafford and Findell, published by the US National Research Council in 2001).
Liz talked more about each strand (see PowerPoint pdf linked above) and drew attention to the fact that all five are of equal importance in the diagram and complement each other. Liz outlined that in some discourse surrounding mastery, there is a great emphasis on procedural fluency and conceptual development, which are both important, but there is a danger that the other three strands are
forgotten. (For more information about NRICH's views on mastery, please see this article.)
We had a go at the task Reach 100 and discussed how it might lend itself to the development of any of the five strands.
Session 3 was an opportunity for delegates to feed back on what they have been trying out in school since we last met. The key points were:


Mary explained that in her school they are continuing to focus on questioning by taking the numbers out of problems and asking "what do you need to know?", then moving on to questions such as "if this was 62, what would the answer be?". Her colleagues have incorporated this sequence into their teaching and are seeing the benefits. Jess suggested that you could leave numbers in, but
remove the question from a problem. Michael talked about making word problems collaborative so that everyone in a group has some information, but not all the information, and some have surplus data. An alternative approach is to slowly reveal more information or give a question and an answer but leave out the middle part. These approaches encourage understanding of mathematics
in terms of relationships and draw attention to variables.
Naomi explained that in her school they had been running booster groups for Y5 which focus on skills and the children have done extremely well, making expected levels of progress. They have found the stages of reasoning we explored in Day 2 very helpful and as a class, they have developed reasoning sentences.
Steph outlined how she has really been focusing on using the counting stick properly and linking NRICH tasks to planning. She wondered how to counter remarks that there is no evidence of differentiation in her children's books, whereas in reality differentiation might have been through use of manipulatives or by teacher questioning. It has made her think more about 'ability'
groupings. Mary suggested that it might be useful to take a photo to stick in the child's book and then the child writes about what s/he has done.
Jess told us about the Y2 cohort in her school who have experienced a 'mastery approach' since the January of Y1. The teachers really focused on numbers within 10 before moving on and this greater time spent has been very worthwhile. However, the teachers are struggling to find the time do enough 'real' problem solving.
Steph shared her thoughts that this course has turned around her original view that it was important to give children contexts in 'real life' . She has come to enjoy maths for the sake of it and to appreciate the importance of a good mathematical 'hook'.
(Members of the group recommended the YouTube clip 'Hollywood Hates Math' which demonstrates how mathematics is negatively portrayed in the media.)
In session 4, Liz showed delegates the new primary Developing Mathematical Habits of Mind page on NRICH, which offers tasks that will develop learners' curiosity, collaborative skills, thoughtfulness and determination. In each of these categories, tasks are grouped according to their mathematical content (number, geometry, measures or statistics).
Liz emphasised that these pages are still in development to some extent, but the idea is that they will help teachers to nurture learners' productive disposition (one of the five strands mentioned above).
In session 5, we looked at the NCETM view of mastery (see the pdf of the PowerPoint slides linked above). More information can be found on the NCETM's Mastery Microsite. We also briefly mentioned the National Association of Mathematics Advisors' (NAMA's) Five Myths of Mastery paper.
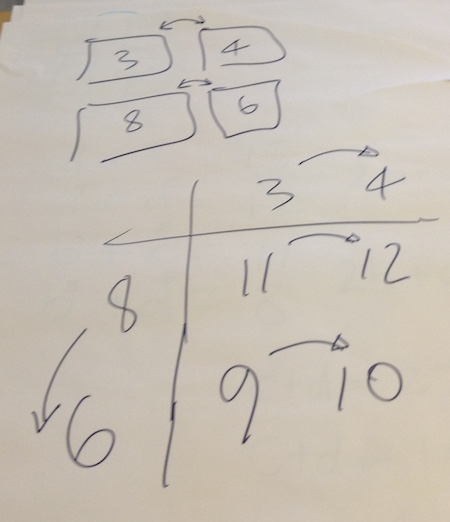
After lunch, session 6 began with the following task: Two spinners each have two single-digit numbers. (All four numbers are different.) The two spinners are spun and the two resulting numbers are added. These are the possible totals:
15, 12, 8, 11
What are the original four numbers?
The following flipcharts show different routes to the solution and different ways of recording:
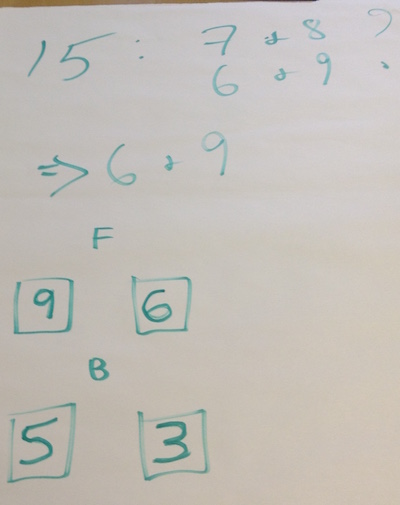

Michael introduced another task. We were given five cards, each with a different number:
14, 15, 16, 17, 62
Comments included that 62 is the total of the four others and that the four others are consecutive numbers. We were encouraged to ask questions, such as what happens when you add up four consecutive numbers? Some of us chose particular examples to work on and we noticed that the sum is always even, also that the sum of the outer two is the same as the sum of the inner two, and that
the answer is always two more than a multiple of four. This flipchart shows some of our recording:

Session 7 gave us chance to share what we have been doing with colleagues in school as a result of this project. Mary explained that she was trying to increase staff confidence and enjoyment of mathematics. She has used the slides linked to this page and has run sessions for colleagues in a similar way to Michael and Liz, modelling questions and problem solving.
Her experience is that they have been very enthusiastic for a few weeks but then the momentum has dropped off so now she is being more focused and concentrating on questioning only (see above). She has also encouraged colleagues to start with a question from a book/scheme etc. but to consider how it can be opened up to provoke more mathematical thinking. Mary said she is working
with Louise and Ben from another local school which has been really valuable.
Naomi reported that she has worked with TAs as well as staff so that they focus less on the 'right' answer and more on explaining and finding possibilities. TAs have also been introduced to NRICH's levels of reasoning we discussed in day 2. She said that it has had a massive impact on the quality of support in the classroom.
In session 8, we had a go at the group task Guess the Houses as an example of one of the resources linked from the Developing Mathematical Habits of Mind pages outlined above. (Liz also mentioned Guess the Dominoes which works in exactly the same way but is in a KS2 context.)
Michael finished the day by sending us off with a task to think about:
Find their sum.
find their difference.
Find the product of their sum and difference.
What do you notice?

