The dog ate my homework!
A practical experiment which uses tree diagrams to help students understand the nature of questions in conditional probability.
Problem
This problem is part of the Great Expectations: Probability through Problems collection. It is designed for classroom use; see the Teachers' Resources for a suggested classroom approach.

A certain teacher, Mr L I Detector, claims he can tell when students are lying about their homework.
This is true.
Unfortunately, he also accuses some students who are telling the truth.
So what are the chances that someone who is accused is actually telling the truth?
You can investigate this question through a practical experiment.
You will need a 6-sided die, and some red, blue, green and yellow multi-link cubes.
The red and blue cubes represent whether a student is telling the truth or lying.
The yellow and green cubes represent whether Mr L I Detector accuses a student or not.
First investigate what happens for one student:
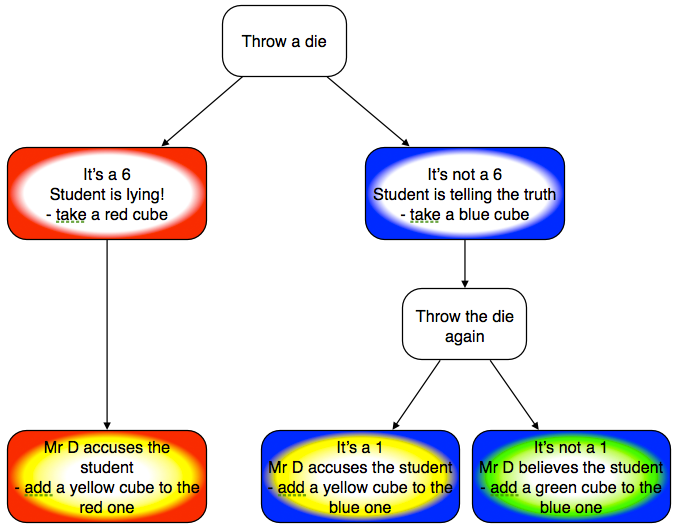
What do each of these mean?
- red and yellow
- blue and yellow
- blue and green
Why can't you have red and green?
Now repeat the experiment 36 times in total. You should end up with 36 pairs of cubes.
Are you surprised by your results?
How do they compare with what you would expect? (You may find this worksheet helpful here).
What proportion of truthful students are accused? So what is the probability of a truthful student being accused?
What proportion of accused students are telling the truth?
Is the probability that a truthful student is accused the same as the probability that an accused student is telling the truth? Are you surprised by this?
You can explore the scenario in this problem using the interactive environment.
Teachers' Resources
Why do this problem?
This problem models the interpretation of statistics for testing for eg. cancer, HIV, pregnancy, DNA at a crime scene, and many other similar situations involving false positives.
Rather than focusing on these potentially difficult topics, however, we have chosen a 'jokey' theme so that students can get into the maths, then appreciate the real world applications through discussion of what the results mean.
Students find tree diagrams, and their interpretation, difficult. The approach used in this problem will help them to become more familiar with tree diagrams, and interpreting them.
Possible approach
Arrange students into groups of 3 or 4. Each group will need a 6-sided die, and some red, blue, green and yellow multi-link cubes. We would suggest you don't hand out any worksheets until students have collected their data (pairs of cubes) and had initial discussion of the results both in their groups and in the class as a whole.
Take the students through the scenario for one student, perhaps using the presentation below:
The Dog Ate My Homework!
Then give them some time to generate data - pairs of multi-link cubes - for 36 students.
Following discussion of the results, students could then record their results on the tree diagram and in the 2-way table provided in this worksheet.
Students could also explore the problem using this interactive environment.
Key questions
How do the experimental results compare with what we would expect?
How many students in total are accused? Are you surprised? Why (not)?
How many innocent students are accused? What proportion of innocent students are accused? So what is the probability that a truthful student is accused?
How many accused students are telling the truth? What proportion of accused students are telling the truth?
Is the probability that a truthful student is accused the same as the probability that an accused student is telling the truth? Are you surprised? Why (not)?
What figures are in both the tree diagram and the 2-way table, which are not?
What are the advantages of the tree diagram? How about the 2-way table? What information can you find easily from each, what is more difficult or impossible to find?
Possible extension
What difference would it make if Mr L I Detector wasn't always right about students who are lying? How could you change the model?
Critique the model. What assumptions does it make? How could you improve it, to make it more realistic?
Probability - It's Deadly Serious is a collection of resources about conditional probability in context, which may provide a suitable extension.
Possible support
All students should be able to carry out the experiment, once they have understood the scenario and done an initial trial together. The worksheet is designed to help students to interpret their results. Students who find the questions above difficult could instead focus on the comparison between experimental and expected results, and on critiquing the model - for instance, is it reasonable to suppose that 1/6 of students would lie about their homework? If not, how could we change the experiment?
